previous: Reelle Funktionen up: Reelle Funktionen next: Spezielle Funktionen

Graph einer Funktion  

Jedem Paar $(x,f(x))$ entspricht ein Punkt in der $xy$-Ebene. Die Menge aller dieser Punkte bildet eine Kurve in dieser Ebene, den sogenannten  Graphen der Funktion.

Wir können Funktionen mit Hilfe des Graphen veranschaulichen. Viele Eigenschaften von Funktionen lassen sich bereits aus deren Graphen herauslesen.

 

Vorgangsweise zum Zeichen (oder Skizzieren):

(1)

Wir überlegen uns zuerst wie der Graph wahrscheinlich aussehen wird. Graphen von elementaren Funktionen und11.3 sollten bereits aus dem Gedächtnis skizziert werden können.

(2)

Wir wählen einen geeigneten Bereich auf der $x$-Achse aus. (Er sollte einen charakteristischen Ausschnitt zeigen.) Achtung auf den Definitionsbereich.

(3)

Wir erstellen eine Wertetabelle und zeichnen die entsprechenden Zahlenpaare in der $xy$-Ebene ein.

(4)

Wir überprüfen, ob aus den gezeichneten Punkten der Verlauf der Kurve ersichtlich ist. Andernfalls verlängern wir die Wertetabelle um einige geeignete Werte.

(5)

Die eingezeichneten Punkte werden in geeigneter Weise miteinander verbunden.

Es ist meist auch hilfreich oder notwendig, charakteristische Punkte -- wie etwa lokale Extrema oder Wendepunkte -- zu berechnen (,,Kurvendiskussion``) und als Stützpunkte zum Zeichnen des Graphen zu verwenden.

BEISPIEL
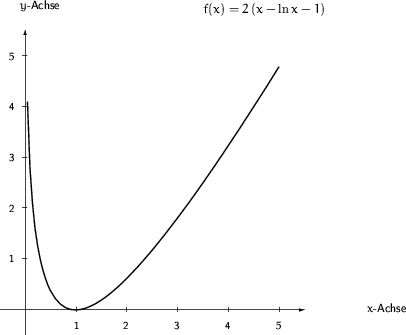
Graph der Funktion $f(x)=2\,(x-\ln x-1)$.

Wertetabelle:

$$x$$ 1 2 3 4 5

$$f(x) 0{,}614 1{,}803 3{,}227 4{,}781$$ n.d.

erweitert durch

$$x 0{,}5 0{,}25 0{,}1 0{,}05$$

$$f(x) 0{,}386 1{,}273 2{,}805 4{,}091$$

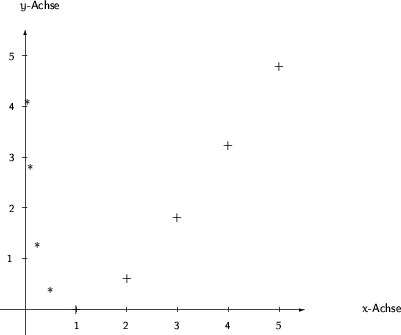
(Graph)

Die Zuordnungsvorschrift einer Funktion kann auch in verschiedenen Intervallen des Definitionsbereichs verschieden definiert sein.

Beim Zeichnen des Graphen so einer Funktion gehen wir in jedem einzelnen der Intervalle genauso wie oben beschrieben vor. Wir müssen dann allerdings an den Intervallgrenzen kennzeichnen, welche Punkte Bestandteil des Graphen sind und welche nicht. Dies geschieht üblicherweise durch $\bullet$ (Bestandteil) und $\circ$ (nicht Bestandteil).

BEISPIEL

 

$f(x)= \left\{ \begin{array} {ll} 1, & \mbox{ für $x<0$}\\ 1-\frac{x^2}{2}, & \mbox{ für $0\leq{}x<1$}\\ x, & \mbox{ für $x\geq{}1$}\\ \end{array} \right.$