previous: Reelle Funktionen up: Reelle Funktionen next: Graph einer Funktion

Reelle Funktionen  

DEFINITION (REELLE FUNKTION)
 Reelle Funktionen sind Abbildungen, in denen sowohl die Definitionsmenge als auch die Wertemenge Teilmengen von ${\mathbb R}$ (meist Intervalle) sind.

Reelle Funktionen sind ein besonders wichtiger Spezialfall von Abbildungen.
(Tatsächlich werden wir im folgenden nur solche Abbildungen behandeln.)

Bei reellen Funktionen wird meist weder Definitionsmenge noch Wertemenge angegeben. In diesem Fall ist die Definitionsmenge die größtmögliche (sinnvolle) Teilmenge von ${\mathbb R}$, in der die Zuordnungsvorschrift definiert ist, und die Wertemenge die  Bildmenge

$$f(D)=\{y\vert y=f(x)\mbox{ für ein }x\in{}D\}$$

(manchmal auch ganz ${\mathbb R}$).

BEISPIEL

$$f(x)=\frac{1}{x}$$

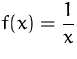
ist eine Abkürzung für

$$f\colon {\mathbb R}\setminus\{0\} \to {\mathbb R}\setminus\{0\},\, x\mapsto f(x)=\frac{1}{x}$$.

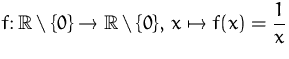(0 kann im Definitionsbereich nicht enthalten sein, da $\frac{1}{0}$ nicht definiert ist.)

BEISPIEL

$$f(x)=\sqrt{x}$$

ist eine Abkürzung für

$$f\colon [0,\infty) \to [0,\infty),\, x\mapsto f(x)=\sqrt{x}$$.

(Die Quadratwurzel ist für negative Zahlen nicht reell.)

BEISPIEL
Der Definitionsbereich einer Nutzenfunktion oder Produktionsfunktion ist eine Teilmenge von $[0,\infty)$.

(Es gibt keine ,,negativen`` Güter.)