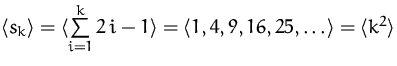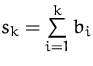 .
.
Wir können nun in unserem Sparbuchbeispiel die ersten ![]() Buchungsbeträge addieren:
Buchungsbeträge addieren:
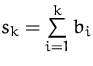 .
.
So eine Summe heißt die ![]() -te
Teilsumme (Partialsumme)
der Folge
-te
Teilsumme (Partialsumme)
der Folge ![]() .
.
DEFINITION (REIHE)
Die Folge ![]() aller
Teilsummen einer Folge
aller
Teilsummen einer Folge
![]() heißt die Reihe der Folge
heißt die Reihe der Folge
![]() .
.
BEISPIEL
Die Reihe der Folge ![]() lautet
(in verschiedenen Darstellungen)
lautet
(in verschiedenen Darstellungen)