previous: Das Gaußsche Eliminationsverfahren up: Das Gaußsche Eliminationsverfahren next: Das Gaußsche Eliminationsverfahren

Lineare Gleichungssysteme  

Ein sehr einfaches Leontief-Modell

Eine Stadt betreibt die Unternehmen öFFENTLICHER VERKEHR, ELEKTRIZITäT und GAS. Die wöchentliche Nachfrage nach diesen Gütern (in Werteinheiten) ist (die Zahlen sind frei erfunden)

Verkehr 7,0

Elektrizität 12,5

Gas 16,5

Jeder Betrieb verbraucht (pro Produktionseinheit) Güter, die er selbst oder andere Betriebe produzieren:

In Tabellenform:

Verbrauch an für Verkehr Elektrizität Gas

Verkehr 0,0 0,2 0,2

Elektrizität 0,4 0,2 0,1

Gas 0,0 0,5 0,1

Wie groß muß die wöchentliche Produktion sein, damit die Nachfrage befriedigt werden kann?

Wir bezeichnen die unbekannte Produktion von Verkehr, Elektrizität und Gas mit $x_1$, $x_2$ bzw. $x_3$.

Für die Produktion muß dann gelten:

Nachfrage = Produktion $-$ interner Verbrauch

$$\begin{array} {ccccccccc} 7,\!0 &=&x_1 &-&(0,\!0\,x_1&+&0,\... ...5&=&x_3 &-&(0,\!0\,x_1&+&0,\!5\,x_2&+&0,\!1\,x_3)\\ \end{array}$$

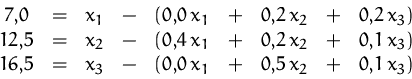
Durch Umformung erhalten wir:

$$\begin{array} {ccccccc} 1,\!0\,x_1 &-& 0,\!2\,x_2 &-& 0,\!2... ...\!0\,x_1 &-& 0,\!5\,x_2 &+& 0,\!9\,x_3 &=& 16,\!5\\ \end{array}$$

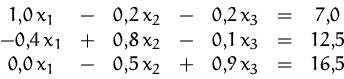
ein lineares Gleichungssystem.

Ein  lineares Gleichungssystem in $m$ Gleichungen und $n$Variablen hat im allgemeinen die Form

$$\begin{array} {rcl} a_{11}\,x_1 + a_{12}\,x_2 + \cdots a_{1... ...}\,x_1 + a_{m2}\,x_2 + \cdots a_{mn}\,x_n &=& b_m\\ \end{array}$$

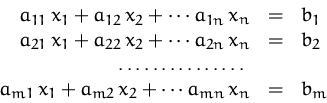
Es gibt drei Lösungsmöglichkeiten:

• Das Gleichungssystem hat genau eine Lösung.
• Das Gleichungssystem ist inkonsistent (nicht lösbar).
• Das Gleichungssystem hat unendlich viele Lösungen.

Aus der Anzahl der Gleichungen und Unbekannten kann noch nicht geschlossen werden, wieviele Lösungen ein Gleichungssystem besitzt.