previous: Logik up: Grundlegendes next: Abbildungen

Mengen  

DEFINITION (MENGE)
Eine  Menge ist eine Sammlung von unterscheidbaren Objekten  (Elementen).

Dabei muß natürlich eindeutig bestimmbar sein, ob ein Objekt zu einer Menge gehört oder nicht.

Mengen werden üblicherweise mit lateinischen Großbuchstaben, deren Elemente mit lateinischen Kleinbuchstaben bezeichnet. Die Tatsache, daß ein Objekt $a$ Element der Menge $A$ist (bzw. nicht ist) bezeichnen wir mit

$\mbox{\ovalbox{$\displaystyle a\in A\quad\mbox{(bzw.\ }a\not\in A\mbox{)}$}}$

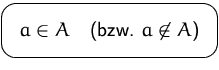
Mengen können definiert werden durch ein

•  aufzählendes Verfahren, z.B.
  

  $A=\{2,4,6,8,10\}$

  oder durch ein

•  beschreibendes Verfahren, z.B.
  

  $A=\{x\vert x\mbox{ ist gerade Zahl kleiner oder gleich }10\}$

Beim Arbeiten mit Mengen nimmt man an, daß alle betrachteten Mengen Teilmengen einer vorgegebenen
 Obermenge $\mathbf{\Omega}$ sind.

SYMBOL BESCHREIBUNG

$$\emptyset$$ leere Menge

$${\mathbb N} \{1,2,3,\ldots\}$$

$${\mathbb N}_0 \{0,1,2,3,\ldots\}$$

$${\mathbb Z}$$ ganze Zahlen

$${\mathbb Q}$$ rationale Zahlen, Bruchzahlen

$$\{\frac{n}{m}\vert n,m\in{\mathbb Z},\,m\not=0\}$$

$${\mathbb R}$$ reelle Zahlen

$$[\,a,b\,] \{x\vert a\leq x\leq b\}$$

$$(\,a,b\,) \{x\vert a< x< b\}$$

$$[\,a,b\,) \{x\vert a\leq x< b\}$$

$${\mathbb R}^+ (0,\infty$$

$${\mathbb R}^+_0 [0,\infty)$$

$${\mathbb R}^2$$ Punkte in der reellen Ebene

$$\{(x,y)\vert x,y\in{\mathbb R}\}$$

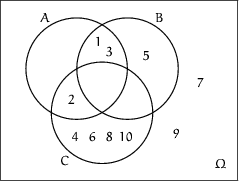
Mengen können durch sogenannte  Venn-Diagramme dargestellt werden.

$A=\{1,2,3\}$
$B=\{1,3,5\}$
$C=\{2,4,6,8,10\}$
$\Omega=\{1,2,3,4,5,6,7,8,9,10\}$

Mengen können (analog zu logischen Aussagen) miteinander verknüpft werden.

SYMBOL DEFINITION BEZEICHNUNG

$$A\cap{}B \{x\vert x\in{}A\wedge{}x\in{}B\}$$ Durchschnitt

$$A\cup{}B \{x\vert x\in{}A\vee{}x\in{}B\}$$ Vereinigung

$$A\setminus{}B \{x\vert x\in{}A\wedge{}x\not\in{}B\}$$ Mengendifferenz

$$\bar{A} \Omega\setminus{}A$$ Komplement

$$A\times B \{(x,y)\vert x\in{}A,\,y\in{}B\}$$ Produktmengen

Mengen können (wie Zahlen) verglichen werden.

SYMBOL BEZEICHNUNG DEFINITION

$$A=B A B x\in{}A\Leftrightarrow{}x\in{}B$$

$$A\subseteq{}B A B x\in{}A\Rightarrow{}x\in{}B$$

$$A B A\cap{}B=\emptyset{}$$

Venn-Diagramme von Mengenverknüpfungen

Für diese Mengenverknüpfungen gibt es -- genauso wie für Addition und Multiplikation von Zahlen -- Rechenregeln.

REGEL BEZEICHNUNG

$$A\cup A = A\cap A = A$$ Idempotenz

$$A\cup\emptyset = A A\cap\emptyset = \emptyset$$ Identität

$$(A\cup B)\cup C = A\cup(B\cup C)$$

$$(A\cap B)\cap C = A\cap(B\cap C)$$ Assoziativität

$$A\cup B = B\cup A A\cap B=B\cap A$$ Kommutativität

$$A\cup(B\cap C) = (A\cup B)\cap(A\cup C)$$

$$A\cap(B\cup C) = (A\cap B)\cup(A\cap C)$$ Distributivität

$$\overline{(A\cup B)}=\bar{A}\cap\bar{B}$$ Gesetz von

$$\overline{(A\cap B)}=\bar{A}\cup\bar{B}$$ De Morgan

$$\bar{A}\cup A= \Omega \bar{A}\cap A=\emptyset$$

$$\bar{\bar{A}}=A$$

Diese Regeln erlauben es, komplizierte Ausdrücke zu vereinfachen.

BEISPIEL

$\begin{array} {l} (A\cap B)\cup\overline{(\bar{A}\cup{}B)}=\\ [0.5ex] (A\ca... ...0.5ex] A\cap(B\cup\bar{B})=\\ [0.5ex] A\cap\Omega=\\ [0.5ex] A \end{array}$