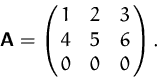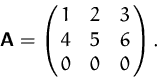previous: Was ist die inverse up: Die inverse Matrix next: Berechnung der inversen Matrix

Existenz der inversen Matrix  

Nicht jede Matrix besitzt eine Inverse. z.B.:

$$\mathsfbf{A}=\pmatrix{ 1 & 2 & 3 \cr 4 & 5 & 6 \cr 0 & 0 & 0 }.$$

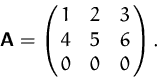
Wir können mit Hilfe des Ranges feststellen, wann eine quadratische Matrix invertierbar ist:

$\mbox{\ovalbox{$\displaystyle \mathsfbf{A}\mbox{ ist \textbf{invertierbar}} \quad\Leftrightarrow\quad \mathsfbf{A}\mbox{ ist \textbf{regulär}}$}}$