Geometrische Interpretation

previous: Vektoren up: Vektoren next: Norm und inneres Produkt

Geometrische Interpretation

eines Vektors 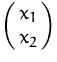$\pmatrix{x_1\cr x_2}$ .

1.: Als Punkt 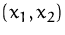in der 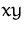-Ebene.
2.: Als Pfeil vom Ursprung zum Punkt
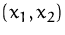
(,,Ortsvektor``).
3.: Als Pfeil mit gleicher Länge, Richtung und Orientierung wie dieser Ortsvektor. (,,Klasse von Pfeilen``)

$\begin{figure} \setlength {\unitlength}{2mm} \begin{picture} (60,35) \thinli... ...} \put(20,17){\makebox(0,0)[rb]{\large$\mathsfbf{x}$}}\end{picture}\end{figure}$

Wir wählen uns immer die Interpration aus, die uns am besten paßt.

(Mit diesen Bildern können wir denken. Rechnen müssen wir aber mit den Formeln.)

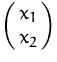$\begin{figure} \setlength {\unitlength}{1.1mm} \mbox{}\\ [-6ex]\mbox{} \begin{... ...,0)[rb]{\large$\mathsfbf{x}+\mathsfbf{y}$}}\end{picture}\end{center}\end{figure}$