Wir wollen komplizierte Funktionen durch möglichst einfache Funktionen approximieren.
Einfachster Fall:
Approximation durch eine lineare Funktion
(totales Differential):
![]()
Etwas weniger einfach:
Approximation durch ein Polynom ![]() .
.
Diese Approximation wird dann ,,möglichst`` gut sein,
falls die Ableitungen von ![]() und
und ![]() übereinstimmen.
übereinstimmen.
ANSATZ:
![]()
Wir bilden nun die Ableitungen an der Stelle ![]()
(![]() lassen wir vorerst weg):
lassen wir vorerst weg):
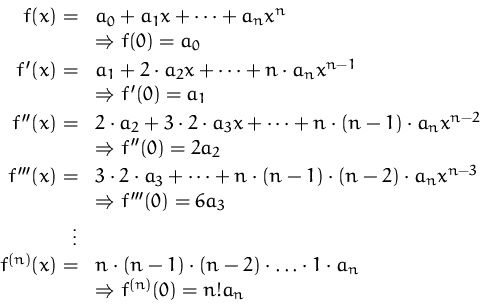
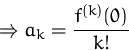
Wir erhalten
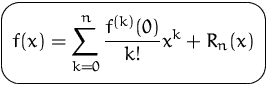
oder allgemeiner:
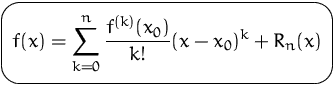
Dieses Polynom (ohne Restglied) heißt das
![]() -te Taylorpolynom der Funktion
-te Taylorpolynom der Funktion ![]() im Punkt
im Punkt ![]() .
.
Die unendliche Reihe (![]() ) (Potenzreihe) heißt
) (Potenzreihe) heißt
die Taylorreihe von ![]() .
.
Der Spezialfall mit ![]() heißt
MacLaurinpolynom bzw. MacLaurinreihe.
heißt
MacLaurinpolynom bzw. MacLaurinreihe.
Wenn ![]() , dann konvergiert die
Taylorreihe gegen
, dann konvergiert die
Taylorreihe gegen ![]() .
(
.
(![]() Taylorentwicklung an der Stelle
Taylorentwicklung an der Stelle ![]() )
)
Das Restglied läßt sich abschätzen.
Lagrange-Form des Restgliedes:
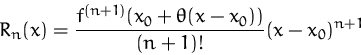
wobei ![]() eine geeignete Zahl ist. (D.h. es gibt so
eine Zahl
eine geeignete Zahl ist. (D.h. es gibt so
eine Zahl ![]() ).
).
Falls ![]() für alle
für alle ![]() und für alle
und für alle ![]() dann ist
dann ist
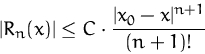
BEISPIEL
Taylorentwicklung von ![]() an der Stelle
an der Stelle ![]() .
.
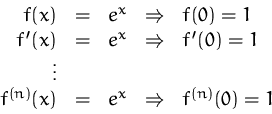
![]()
Diese Taylorreihe konvergiert für alle ![]()
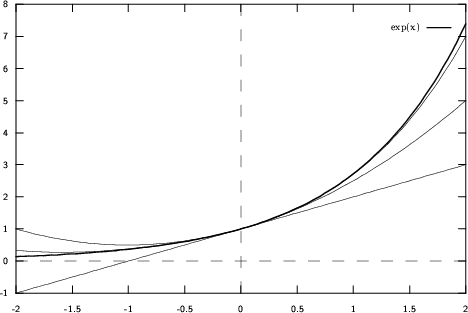
Es gibt aber auch Taylorreihen, die nicht für alle ![]() konvergieren.
konvergieren.
Es gilt jedoch:
Falls eine Taylorreihe für ein ![]() mit
mit ![]() konvergiert, so konvergiert sie für alle
konvergiert, so konvergiert sie für alle ![]() mit
mit ![]() . Das
größtmögliche derartige
. Das
größtmögliche derartige ![]() heißt der Konvergenzradius der
Taylorreihe.
heißt der Konvergenzradius der
Taylorreihe.
BEISPIEL
Taylorreihe für ![]() an der Stelle
an der Stelle ![]() .
.
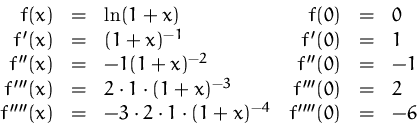
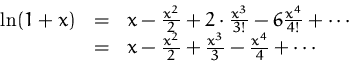
Hier ist der Konvergenzradius ![]() (ohne Beweis).
(ohne Beweis).
Indiz:
![]() ist für
ist für ![]() nicht definiert, die Taylorreihe
hingegen schon.
nicht definiert, die Taylorreihe
hingegen schon.
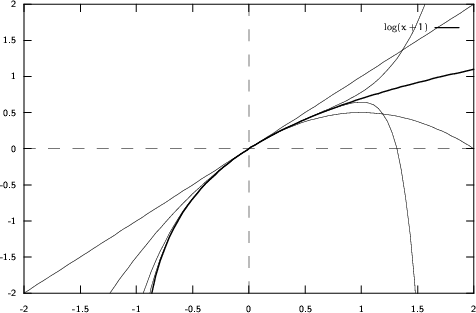
Es gibt sogar Funktionen, deren Taylorreihe für kein einziges
![]() konvergiert.
konvergiert.
Einige wichtige Taylorreihen:
| MacLaurinreihe | ||
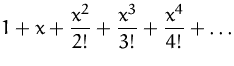 |
||
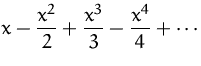 |
1 | |
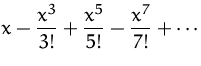 |
||
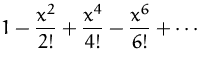 |
||
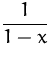 |
1 |
Wir können Taylorreihen
BEISPIEL
Wir erhalten die Taylorreihe von ![]() durch Multiplizieren
der Taylorreihe von
durch Multiplizieren
der Taylorreihe von ![]() mir der Taylorreihe von
mir der Taylorreihe von ![]() an der Stelle
an der Stelle
![]() :
:
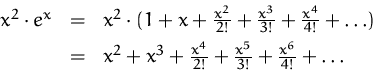
BEISPIEL
Die Taylorreihe von ![]() erhalten wir durch Substituieren
(Einsetzen) von
erhalten wir durch Substituieren
(Einsetzen) von ![]() in die Taylorreihe von
in die Taylorreihe von ![]() an der Stelle
an der Stelle ![]() :
:
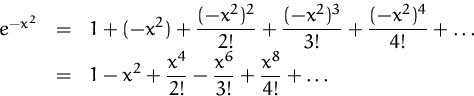
BEISPIEL
Die MacLaurinreihe von ![]() lautet
lautet
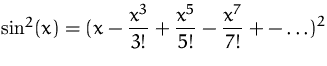
![]()
![]()
![]()
![]()
![]()
= ![]()