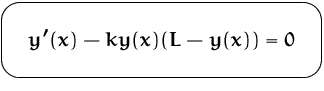
![]()
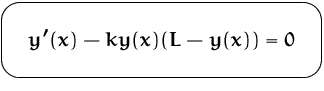
![]()
Differentialgleichung des beschränkten exponentiellen
Wachstums
Lösung durch Trennung der Variablen:
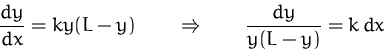
Integrieren (linke Seite):
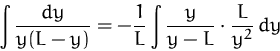

![]()
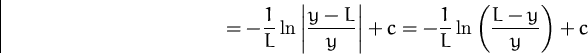
Wir erhalten damit insgesamt
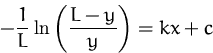
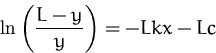
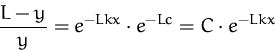
![]()
![]()
allgemeine Lösung der logistischen DG
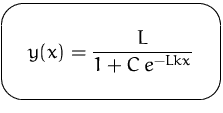
Die Lösung der logistischen DG hat einen Wendepunkt, wenn
![]() .
.
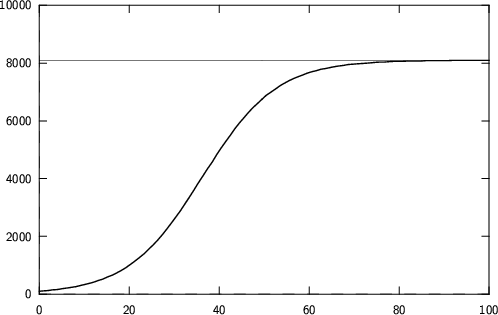
BEISPIEL
In einer Stadt mit 8100 Einwohner gibt es eine Grippeepidemie.
Als die Krankheit erkannt wird, sind 100 Bewohner betroffen,
20 Tage später sind es bereits 1000.
Wie läßt sich der Epidemieverlauf beschreiben?
Wir nehmen für die Anzahl ![]() der betroffenen Einwohner ein beschränktes
expontielles Wachstum an, mit
der betroffenen Einwohner ein beschränktes
expontielles Wachstum an, mit ![]() .
.
![]()
![]()
![]()
![]()
![]()