




previous: Trennung der Variablen
up: Einfache DG erster Ordnung
next: Inhomogene lineare DG erster
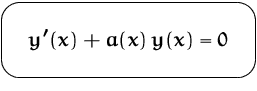
Lösung: (durch Trennung der Variablen)
BEISPIEL
Lösung von 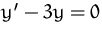
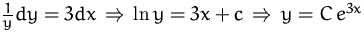
BEISPIEL
Lösung von 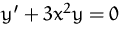
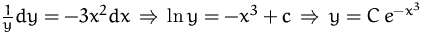





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
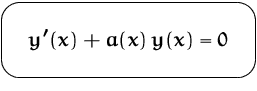
![]()
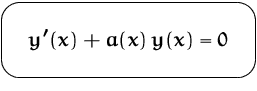
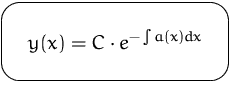
![]()
![]()
![]()
![]()