previous: Was ist eine Differentialgleichung? up: Differentialgleichungen next: Einfache DG erster Ordnung

Ein einfaches Modell  

(nach Domar, 1946)

Untersuchen die Investitionen $I(t)$ im Laufe der Zeit $t$.$K(t)$ ist der Kapitalstock zum Zeitpunkt $t$ ist.

$$\frac{dK}{dt}=I$$

Treffen Annahmen:

Eine Änderung der Investitionen bewirkt

1.

eine Änderung der Kaufkraft $Y(t)$:

$$\frac{dY}{dt} = \frac{dI}{dt} \cdot \frac{1}{s} \eqno{(A1)}$$

2.

eine Änderung der Produktionskapazität $\kappa(t)$.
Modell: Konstantes Kapazitäts-Kapital-Verhältnis:

$$\frac{\kappa(t)}{K(t)} = \varrho \quad \mbox{(= konstant)} \eqno{(A2)}$$

Das Modell befindet sich in Gleichgewicht, falls Kaufkraft und Produktionskapazität übereinstimmen:

$$Y = \kappa\eqno{(G)}$$

Starten von Gleichgewichtszustand ($t = 0$).

Welche Investitionsfunktion $I(t)$ erfüllt die Gleichgewichtsbedingung für alle Zeiten?

Aus $(G)$ erhalten wir

$$\frac{dY}{dt} = \frac{d \kappa}{dt}$$

und aus $(A2)$

$$\kappa = \varrho K \quad\Rightarrow\quad \frac{d\kappa}{dt} =\varrho\, \frac{dK}{dt} = \varrho I$$

Eingesetzt in $(A1)$

$$\frac{dI}{dt} \cdot\frac{1}{s} = \frac{dY}{dt} = \frac{d \kappa}{dt} = \varrho I$$

oder

$\mbox{\ovalbox{$\displaystyle \frac{dI}{dt} = \varrho\, s\, I$}}$ $\qquad\qquad\mbox{bzw.}\qquad\qquad$ $$\frac{1}{I}\frac{dI}{dt} = \varrho\, s$$

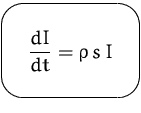
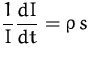
Wir erhalten eine DG erster Ordnung.

Lösung des Modells:

Diese Gleichung muß für alle $t\gt$ erfüllt sein.

$$\int \frac{1}{I} \frac{dI}{dt} dt = \int \varrho \, s\, dt$$

linke Seite:
Substitution: $I = I(t) \,\Rightarrow\, dI = I'(t)dt$

$$\int \frac{1}{I} dI = \ln I + c_1$$

rechte Seite:

$$\int \varrho\, s\, dt = \varrho\, s \, t + c_2$$

Insgesamt:

$$\ln I = \varrho \, s \, t + c$$

und

$$I = e^{\varrho s t} \cdot e^c = A e^{\varrho s t}$$

 allgemeine Lösung:

$$I (t) = A\, e^{\varrho s t}$$

$A$ ist eine beliebige Konstante $\gt$.

 spezielle Lösung des  Anfangswertproblems

$$\left. \begin{array} {l} I' = \rho s \cdot I\\ I(0)=I_0\\ \end{array} \right\}$$

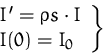
Lösen durch Einsetzen in allgemeine Lösung:

$I_0 = I(0) = A \, e^{\rho s 0} =A$

$\mbox{\ovalbox{$\displaystyle I(t) = I_0 e^{\rho s t}$}}$

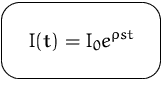
Verfizieren der Lösung (Probe):

$$I' = \varrho s \, I_0\, e^{\varrho s t}$$

$$\frac {1}{I} \cdot I' = \frac {1}{I_0 \, e^{\varrho s t}} \cdot \varrho s \, I_0 \, e^{\varrho s t} = \varrho s$$