Eine Funktion
DEFINITION (STAMMFUNKTION)
Eine Funktion ![]() heißt
Stammfunktion einer Funktion
heißt
Stammfunktion einer Funktion
![]() , falls
, falls ![]() .
.
Berechnung:

BEISPIEL
Wir suchen die Stammfunktion von ![]() .
.
Vermuten:
![]()
Verifizieren:
![]()
![]()
Aber auch:
![]()
oder:
![]()
Dieses ![]() heißt Integrationskonstante.
heißt Integrationskonstante.
Zur Erleichterung gibt es Tabellen mit bekannten Stammfunktionen, sogenannten Grundintegralen.
| Funktion |
Stammfunktion |
|
Die Stammfunktion wird auch mit
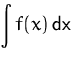 bezeichnet und dabei -- nicht
ganz richtig -- als das
unbestimmte Integral
der Funktion
bezeichnet. Das Suchen der Stammfunktion heißt daher auch
Integrieren.
bezeichnet und dabei -- nicht
ganz richtig -- als das
unbestimmte Integral
der Funktion
bezeichnet. Das Suchen der Stammfunktion heißt daher auch
Integrieren.
Zum Auffinden von Stammfunktionen stehen ein paar Werkzeuge zur Verfügung, die es uns erlauben, die Stammfunktionen von komplizierten Funktionen auf Grundintegrale zurückzuführen ( Integrationsverfahren).
| Bezeichnung | Verfahren | |
| Partielles | 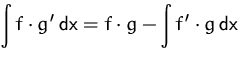 |
|
| Integrieren | ||
| Substitution | 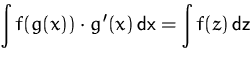 |
|
| mit |
BEISPIEL PARTIELLES INTEGRIEREN
Wir suchen die Stammfunktion von ![]() .
.
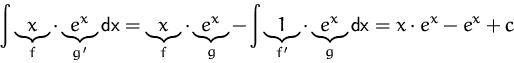
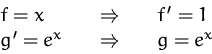
BEISPIEL SUBSTITUTION
Wir suchen die Stammfunktion von ![]() .
.

![]()
Es kann auch sein, daß diese Integrationsverfahren mehrmals angewendet werden müssen.
BEISPIEL
Wir suchen die Stammfunktion von ![]() . Partielles Integrieren:
. Partielles Integrieren:
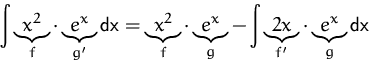
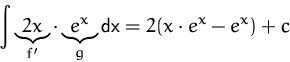
![]()
Für das Suchen von Stammfunktionen gibt es keine ,,Kochrezepte``.
Es gibt Funktionen, deren Stammfunktionen sich nicht durch elementare Funktionen ausdrücken lassen.
BEISPIEL
Die Stammfunktion von ![]() läßt sich nicht durch
elementare Funktionen ausdrücken.
läßt sich nicht durch
elementare Funktionen ausdrücken.
(Diese Funktion ist aber trotzdem in der Statistik von großer Bedeutung.)