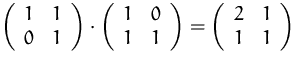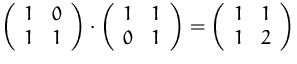Das Produkt zweier Matrizen ![]() und
und ![]() ist nur dann
definiert, wenn die Anzahl der Spalten der ersten Matrix gleich der
Anzahl der Zeilen der zweiten Matrix ist.
ist nur dann
definiert, wenn die Anzahl der Spalten der ersten Matrix gleich der
Anzahl der Zeilen der zweiten Matrix ist.
D.h., wenn ![]() eine
eine ![]() -Matrix ist, so muß
-Matrix ist, so muß ![]() eine
eine
![]() -Matrix sein.
-Matrix sein.
Die Produktmatrix ![]() ist dann eine
ist dann eine
![]() -Matrix.
-Matrix.
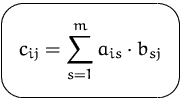
BEISPIEL
Seien
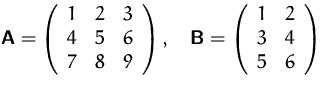
Zur Berechnung der Produktmatrix
![]() ist es sinnvoll, die Matrizen
höhenversetzt nebeneinander zu schreiben (Falksches Schema).
ist es sinnvoll, die Matrizen
höhenversetzt nebeneinander zu schreiben (Falksches Schema).
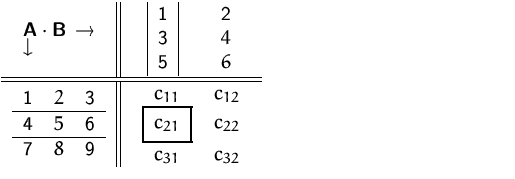
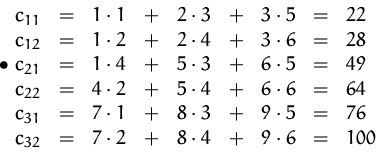
Also
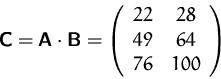
Die Matrizenmultiplikation ist nicht kommutativ.

BEISPIEL
![]() muß nicht immer existieren, falls
muß nicht immer existieren, falls
![]() existiert.
existiert.
![]() und
und
![]() existieren nur dann, wenn
existieren nur dann, wenn
![]() eine
eine ![]() -Matrix und
-Matrix und ![]() eine
eine ![]() -Matrix ist.
-Matrix ist.
Falls ![]() eine
eine ![]() -Matrix und
-Matrix und ![]() eine
eine
![]() -Matrix ist, dann ist
-Matrix ist, dann ist ![]() eine
eine ![]() -Matrix und
-Matrix und ![]() eine
eine ![]() -Matrix.
Also
-Matrix.
Also ![]() , falls
, falls
![]() .
.
Auch wenn wir zwei quadratische Matrizen multiplizieren, ist die Matrizenmultiplikation meist nicht kommutativ.
BEISPIEL