previous: Degenerierte Basislösung up: Spezialfälle next: Zulässiger Bereich leer

Unbeschränkter zulässiger Bereich  

BEISPIEL FORTSETZUNG
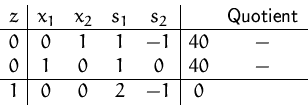
Beim nächsten Pivotschritt erhalten wir das Tableau:

$$\begin{array} {c\vert cccc\vert cc} z & x_1 & x_2 & s_1 & s... ...& 0 & 40 & - \\ \hline 1 & 0 & 0 & 2 & -1 & 0 & \end{array}$$

mit der Basislösung $(x_1,x_2;s_1,s_2) = (40,40;0,0)$.

Wir haben die maximale zulässige Basislösung noch nicht gefunden, da nicht alle Einträge in der Zielfunktionszeile $\geq 0$ sind.

Für den nächsten Pivotschritt müssen wir die $s_2$-Spalte als Pivotspalte wählen. In dieser Pivotspalte sind aber alle Einträge $\leq 0$.

Das Optimierungsproblem ist daher unbeschränkt. Es gibt keine Lösung. (Abbildung, oben).