BEISPIEL
Wir wollen das lineare Optimierungsproblem
(Abbildung, unten).
![]()
![]()
Anfangs-Simplex-Tableau:
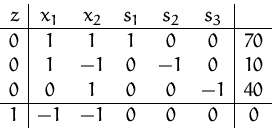
Die Basislösung ![]() ist nicht zulässig. Wir müssen daher den
Zwei-Phasen-Simplex-Algorithmus verwenden.
ist nicht zulässig. Wir müssen daher den
Zwei-Phasen-Simplex-Algorithmus verwenden.
1. Phase:
Wir benötigen zwei Hilfsvariable und ersetzen die
Zielfunktion ![]() durch
durch ![]() :
:

![]()
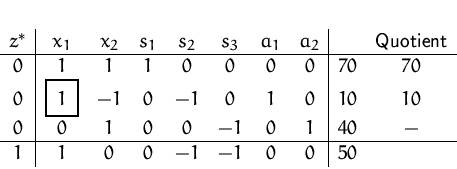
Minimieren der Hilfsfunktion ergibt


Wir haben das Minimum erreicht, da alle Einträge in der
Zielfunktionszeile ![]() sind. Aber
sind. Aber ![]() .
.
Der zulässige Bereich ist leer. Es gibt keine Lösung des linearen Optimierungsproblem, die alle Nebenbedingungen erfüllt.