previous: Unendlich viele Lösungen up: Spezialfälle next: Unbeschränkter zulässiger Bereich

Degenerierte Basislösung  

Eine Basislösung heißt  degeneriert, wenn eine der Basisvariablen gleich 0 ist.

In diesem Fall ändert ein Pivotschritt nur die Menge der Basisvariablen, nicht jedoch die Basislösung.

BEISPIEL
Wir wollen das lineare Optimierungsproblem
(Abbildung, oben).

$$z(x_1,x_2) = x_1 + x_2 \quad\longrightarrow\quad\max$$

$$x_1\leq 40,\qquad x_1 - x_2\leq 0,\qquad x_1,x_2\geq 0$$

mit dem Simplex-Algorithmus lösen.

Anfangs-Simplex-Tableau:

$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert cccc\ver... ...& 1 & 0 & 0 \\ \hline 1 & -1 & -1 & 0 & 0 & 0 & \end{array}$$

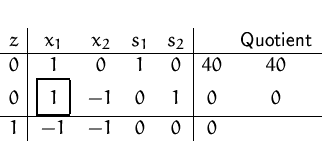
Die (zulässige) Basislösung ist

$(x_1,x_2;s_1,s_2) = (0,0;40,0)$.

Nach dem ersten Pivotschritt erhalten wir:

$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert cccc\ver... ... & 1 & 0 & - \\ \hline 1 & 0 & -2 & 0 & 1 & 0 & \end{array}$$

mit der Basislösung

$(x_1,x_2;s_1,s_2) = (0,0;40,0)$,

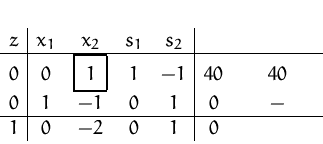
d.h. die Basislösung hat sich nicht verändert.

Allerdings sind die Basisvariablen jetzt $x_2$ und $s_2$, anstatt $x_1$ und $x_2$.

In beiden Tableaus ist eine der beiden Basisvariablen gleich 0.