previous: Spezialfälle up: Spezialfälle next: Degenerierte Basislösung

Unendlich viele Lösungen  

Lösen des lineare Optimierungsproblem (Abbildung).

$$z(x_1,x_2)=2\,x_1+x_2 \quad\longrightarrow\quad\max$$

$$2\,x_1 + x_2 \leq 100,\qquad x_1 + x_2 \leq 80,\qquad x_1 \leq 40,$$

$$x_1,x_2\geq 0$$

mit dem Simplex-Algorithmus:

$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert ccccc\ver... ...0 & 0&0&1 & 40&40\\ \hline 1 & -2&-1 & 0&0&0 & 0 &\end{array}$$

Die Basislösung $(x_1,x_2;s_1,s_2,s_3)=(0,0;100,80,40)$ ist zulässig. Wir können daher das Standardverfahren verwenden.

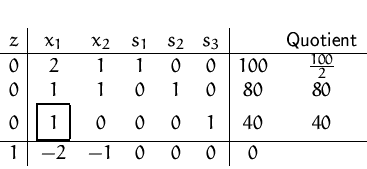
Nach zwei Pivotschritten erhalten wir:

$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert ccccc\ver... ... & 0&0&1 & 40& 40\\ \hline 1 & 0&0 & 1&0&0 & 100 &\end{array}$$

Die maximale zulässige Basislösung ist

$(x_1,x_2;s_1,s_2,s_3) = (40,20;0,20,0)$.

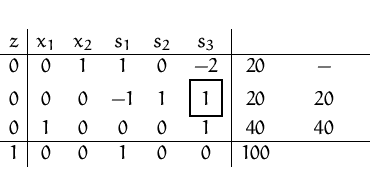
Im Tableau ist aber nur mehr ein (statt zwei) Koeffizienten in der ZFZ ungleich Null. Wir können noch einen Pivotschritt ausführen und erhalten eine weitere maximale zulässige Basislösung:

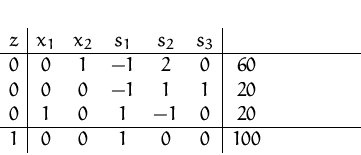
$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert ccccc\ver... ...&0 & 1&-1&0 & 20&\\ \hline 1 & 0&0 & 1&0&0 & 100 &\end{array}$$

$(x_1,x_2;s_1,s_2,s_3) = (20,60;0,0,20)$