previous: Die Standardform
up: Die Standardform
next: Das Standard-Maximierungsproblem
- (1)
- Wir bringen alle Konstanten auf die rechte Seite und auf
positives Vorzeichen.
- (2)
- Jede ,,
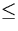 ``-Ungleichung bringen wir durch Addition
einer Schlupfvariablen in Gleichungsform.
``-Ungleichung bringen wir durch Addition
einer Schlupfvariablen in Gleichungsform.
- (3)
- Jede ,,
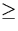 ``-Ungleichung (außer die
Nichtnegativitätsbedingungen!) bringen wir durch Subtraktion einer
Schlupfvariablen in Gleichungsform.
``-Ungleichung (außer die
Nichtnegativitätsbedingungen!) bringen wir durch Subtraktion einer
Schlupfvariablen in Gleichungsform.
- (4)
- Jede Variable
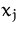 , die nicht die Nichtnegativitätsbedingung
erfüllt, stellen wir als Differenz zweier nicht-negativer Variablen
, die nicht die Nichtnegativitätsbedingung
erfüllt, stellen wir als Differenz zweier nicht-negativer Variablen
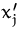 und
und 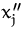 dar:
dar:

- (5)
- Wir fassen auch
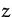 als Variable auf und fügen
die zu optimierende Funktion in Form der Gleichung
als Variable auf und fügen
die zu optimierende Funktion in Form der Gleichung
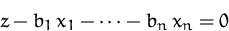
als letzte Zeile (Zielfunktionszeile)
in unser lineares Gleichungssystem und bringen dieses in Matrixform
(Simplex-Tableau).
Wenn eine Zeile (außer der Zielfunktionszeile) keine Schlupfvariable
enthält, d.h. die entsprechende Nebenbedingung ist eine Gleichung,
dann müssen wir das Tableau noch geeignet umformen:
-
- Wir wählen die Zeile ohne Schlupfvariable als Pivotzeile, und
eine Spalte, in der diese Zeile ein Element ungleich Null enthält, als
Pivotspalte, und führen einen Pivotschritt aus.
Alle Zeilen (außer der Zielfunktionszeile), die dabei eine negative
Konstante in der rechten Spalte erhalten, werden anschließend mit
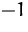 multipliziert.
multipliziert.
BEISPIEL
Wir bringen das lineare Optimierungsproblem auf
Standardform und stellen das Anfangs-Simplex-Tableau auf:
![\begin{displaymath}
\begin{array}
{rcl}
z(x_1,x_2,x_3)=2\,x_1-5\,x_2+x_3 &\long...
...1 + 4\,x_3 &=& 40\\ [0.5ex]
x_1,\,x_2 &\geq& 0\\ \end{array} \end{displaymath}](img1477.gif)
(1) Wir multiplizieren die zweite Ungleichung mit 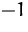 :
:
![\begin{displaymath}
\begin{array}
{rcl}
z = 2\,x_1-5\,x_2+x_3 &\longrightarrow&...
...1 + 4\,x_3 &=& 40\\ [0.5ex]
x_1,\,x_2 &\geq& 0\\ \end{array} \end{displaymath}](img1478.gif)
(2) und (3).
Durch Addition und Subtraktion von
Schlupfvariablen bringen wir die Ungleichungen in Gleichungsform:
![\begin{displaymath}
\begin{array}
{rrrrrrcr}
&&&&&\makebox[0pt][r]{$z=2\,x_1-5\...
...0pt][r]{$x_1,\,x_2,\,s_1,\,s_2,\,s_3$} &\geq& 0\\ \end{array} \end{displaymath}](img1479.gif)
(4) 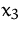 erfüllt nicht die Nichtnegativitätsbedingung:
erfüllt nicht die Nichtnegativitätsbedingung:
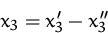
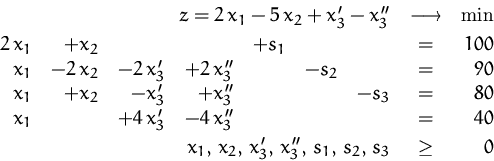
(5)
Einfügen der Zielfunktion:
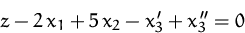
In Matrixform (Simplex-Tableau):
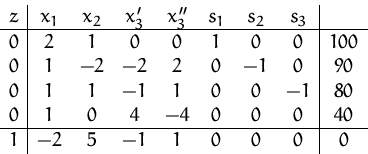
(6) Die vierte Zeile enthält keine Schlupfvariable.
Wir machen einen Pivotschritt (Pivotelement in der 4. Zeile und
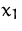 -Spalte).
-Spalte).
Das Anfangs-Simplex-Tableau lautet daher:
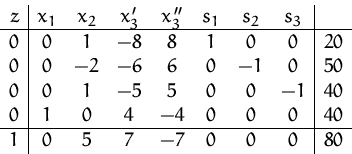





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![]()
![]()
![]()
![]()
![]() multipliziert.
multipliziert.
![\begin{displaymath}
\begin{array}
{rcl}
z(x_1,x_2,x_3)=2\,x_1-5\,x_2+x_3 &\long...
...1 + 4\,x_3 &=& 40\\ [0.5ex]
x_1,\,x_2 &\geq& 0\\ \end{array} \end{displaymath}](img1477.gif)
![]() :
:
![\begin{displaymath}
\begin{array}
{rcl}
z = 2\,x_1-5\,x_2+x_3 &\longrightarrow&...
...1 + 4\,x_3 &=& 40\\ [0.5ex]
x_1,\,x_2 &\geq& 0\\ \end{array} \end{displaymath}](img1478.gif)
![\begin{displaymath}
\begin{array}
{rrrrrrcr}
&&&&&\makebox[0pt][r]{$z=2\,x_1-5\...
...0pt][r]{$x_1,\,x_2,\,s_1,\,s_2,\,s_3$} &\geq& 0\\ \end{array} \end{displaymath}](img1479.gif)
![]() erfüllt nicht die Nichtnegativitätsbedingung:
erfüllt nicht die Nichtnegativitätsbedingung:
![]()
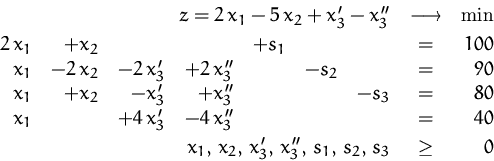
![]()
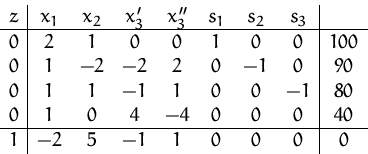
![]() -Spalte).
-Spalte).