previous: Das Simplextableau up: Der Simplex-Algorithmus next: Die Standardform

Pivotschritte  

(1)

Wir wählen als  Pivotspalte immer die Spalte mit dem kleinsten Eintrag in der Zielfunktionszeile.

(2)

Wir bilden die Quotienten aus den Konstanten in der Spalte ganz rechts und den entsprechenden Einträgen in der Pivotspalte. Die Zeile mit dem kleinsten nichtnegativen Quotienten wählen wir als  Pivotzeile. Das Element in der Pivotspalte und Pivotzeile heißt  Pivotelement.

(3)

Wir dividieren die Pivotzeile durch das Pivotelement und subtrahieren von jeder anderen Zeile ein geeignetes Vielfaches der Pivotzeile sodaß die entsprechenden Komponenten in der Pivotspalte gleich 0 werden ( Pivotschritt).

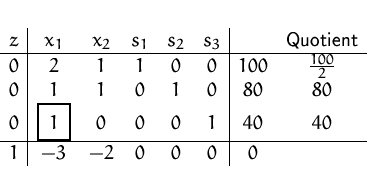
Bei dieser Umformung wird aus einer Basisvariable eine ,,Nicht-Basisvariable`` und aus einer ,,Nicht-Basisvariable`` eine Basisvariable.

Durch so einen Pivotschritt gelangen wir zu einem benachbarten Eckpunkt des zulässigen Bereichs, in dem der Zielfunktionswert verbessert wird.

$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert ccccc\ver... ...0 & 0&0&1 & 40&40\\ \hline 1 & -3&-2 & 0&0&0 & 0 &\end{array}$$

$$Z1 \leftarrow Z1 - 2\times Z3,\quad Z2 \leftarrow Z2 - Z3,\quad ZFZ \leftarrow ZFZ + 3\times Z3$$

$$\begin{array} {c\vert ccccc\vert cc} z & x_1&x_2 & s_1&s_2&... ...0 & 0&0&1 & 40& \\ \hline 1 & 0&-2 & 0&0&3 & 120 &\end{array}$$

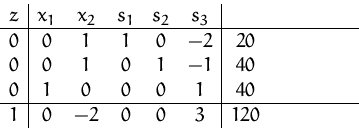
Die Basisvariablen dieses Tableaus sind $x_1$, $s_1$ und $s_2$.Die (zulässige) Basislösung lautet:

$$(40,0;20,40,0)$$

Die Pivotspalte bestimmt, in welche Richtung der nächste Eckpunkt gesucht wird.

Durch die Auswahl einer Spalte mit negativem Eintrag in der Zielfunktionszeile wird gewährleistet, daß der Zielfunktionswert zunimmt. (Die Spalte mit dem kleinsten Eintrag zu nehmen ist Konvention. Sie verspricht den schnellsten Weg zum Maximum.)

Als Pivotzeile wird immer die Nebenbedingung mit der stärksten Einschränkung gewählt. Dadurch wird garantiert, daß wir nicht aus dem zulässigen Bereich herausfallen.

Die  optimale zulässige Basislösung ist erreicht, wenn alle Einträge in der ZFZ nicht-negativ sind.

$$z -2\,x_2 + 3\,s_3 = 120 \quad\Leftrightarrow\quad z = 120 + 2\,x_2 - 3\,s_3$$

Da $x_2 = s_3 = 0$ kann für ein $x_2 \gt 0$ der Zielfunktionswert erhöht werden.

Die Zielfunktion darf daher nie von Basisvariablen abhängen.

$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert ccccc\ver... ...0 & 0&0&1 & 40&-\\ \hline 1 & 0&-2 & 0&0&3 & 120 &\end{array}$$

$$Z2 \leftarrow Z2 - Z1,\quad ZFZ \leftarrow ZFZ + 2\times Z2$$

$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert ccccc\ver... ... & 0&0&1 & 40&40\\ \hline 1 & 0&0 & 2&0&-1 & 160 &\end{array}$$

$$Z1 \leftarrow Z1 + 2\times Z2,\quad Z3 \leftarrow Z3 - Z2,\quad ZFZ \leftarrow ZFZ + Z2$$

$$\setlength {\fboxsep}{2mm} \begin{array} {c\vert ccccc\ver... ...1&0 & 1&-1&0 & 20&\\ \hline 1 & 0&0 & 1&1&0 & 180&\end{array}$$

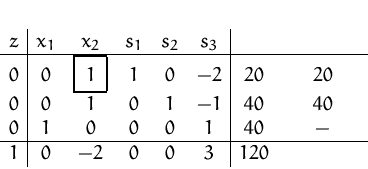
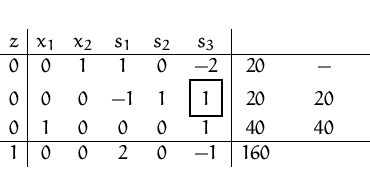
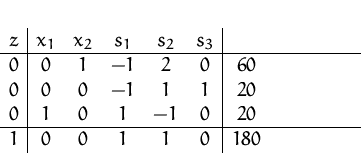
Im letzten Tableau sind alle Komponenten in der Zielfunktionszeile $\geq 0$ (der Eintrag in der Konstantenspalte wird dabei nicht berücksichtigt werden). Wir haben das Maximum erreicht:

$$z + s_1 + s_2 = 180 \quad\Leftrightarrow\quad z = 180 - s_1 - s_2$$

Da $s_1, s_2\geq 0$, würde jede Änderung den Zielfunktionswert verringern.

Die Basisvariablen dieses Tableaus sind $x_1$, $x_2$ und $s_3$.(Das sind die Spalten, in denen Einheitsvektoren stehen.) Alle anderen Variablen ($s_1$ und $s_2$) setzen wir gleich Null.

Die maximale zulässige Basislösung lautet daher:

$$(20,60;0,0,20)$$

Das Maximum liegt somit im Punkt $(20,60)$.Aus der Zielfunktionszeile erhalten wir den optimalen Zielfunktionswert:

$$z_{\max} = 180$$