previous: Der Algorithmus up: Der Simplex-Algorithmus next: Pivotschritte

Das Simplextableau  

Wir schreiben das lineare Gleichungssystem in Matrixform an, wobei wir auch $z$ als Variable auffassen und die Zielfunktion, in Form der Gleichung

$$z-3\,x_1-2\,x_2=0,$$

als letzte Zeile hinzufügen.

Wir erhalten dadurch das  Anfangs-Simplex-Tableau

$$\begin{array} {r\vert rrrrr\vert r} z&x_1&x_2&s_1&s_2&s_3&\... ...& 1&0 & 0&0&1 & 40\\ \hline 1 &-3&-2& 0&0&0 & 0\\ \end{array}$$

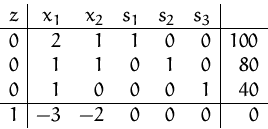
Wenn wir in diesem Tableau $x_1=0$ und $x_2=0$ setzen, dann können wir die Variablen $s_1$, $s_2$, $s_3$ und $z$ sofort aus dem Tableau ablesen:

$$s_1=100,\, s_2=80,\, s_3=40\mbox{ und }z=0$$

Die Variablen $s_1$, $s_2$ und $s_3$ sind die  Basisvariablen dieses Tableaus.