




previous: Der Simplex-Algorithmus
up: Der Simplex-Algorithmus
next: Der zulässige Bereich
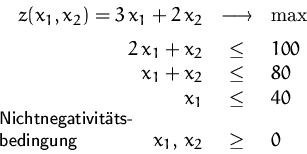
Wir führen für jede Ungleichung unseres linearen Optimierungsproblems
(vgl.)
eine neue Variable ( Schlupfvariable) ein und ersetzen das
,,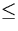 ``-Zeichen durch ein
Gleichheitszeichen:
``-Zeichen durch ein
Gleichheitszeichen:
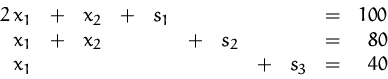
Eine Schlupfvariable ist genau dann gleich Null, wenn der Punkt
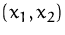 auf dem Rand der entsprechenden Halbebene liegt.
auf dem Rand der entsprechenden Halbebene liegt.
Die Schlupfvariable 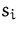 ist genau dann
ist genau dann 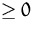 , falls die entsprechende
Nebenbedingung erfüllt ist, und
, falls die entsprechende
Nebenbedingung erfüllt ist, und 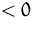 falls nicht.
falls nicht.





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
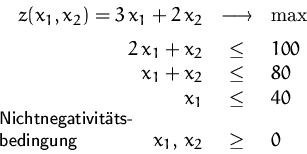
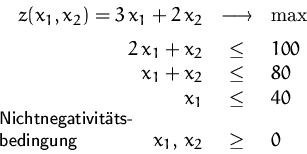
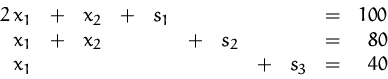
![]() auf dem Rand der entsprechenden Halbebene liegt.
auf dem Rand der entsprechenden Halbebene liegt.
![]() ist genau dann
ist genau dann ![]() , falls die entsprechende
Nebenbedingung erfüllt ist, und
, falls die entsprechende
Nebenbedingung erfüllt ist, und ![]() falls nicht.
falls nicht.
![\begin{figure}
\setlength {\unitlength}{1.0mm}
\begin{picture}
(110,120)
\tex...
...,100){\circle*{2}}
\put(37,100){\makebox(0,0)[l]{$N$}}\end{picture}\end{figure}](img1434.gif)