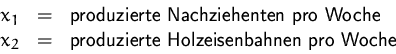
Die Toys&Joys Ges.m.b.H. erzeugt Nachziehenten und Spielzeugeisenbahnen aus Holz.
Eine Nachziehente kann um 27 GE verkauft werden. Die Materialkosten pro Ente betragen 10 GE, sonstige variable Kosten 14 GE. Der Verkaufspreis für die Eisenbahn ist 21 GE, die Materialkosten und sonstigen variablen Kosten pro Eisenbahn betragen 9 GE bzw. 10 GE.
Bei der Produktion sind zwei Arbeitsgänge notwendig: Lackieren und Montieren der Einzelteile. Das Lackieren der Teile einer Ente benötigt 2 Stunden, die Montage 1 Stunde. Für die Eisenbahn werden jeweils 1 Stunde benötigt.
Jede Woche können beliebig viele Rohmaterialien verbraucht werden. Für das Lackieren stehen allerdings pro Woche nur 100 Stunden, für die Montage höchstens 80 Stunden zur Verfügung. Außerdem ist die Nachfrage nach Nachziehenten mit 40 Stück pro Woche begrenzt.
Wir suchen ein Produktionsprogramm, daß den wöchentlichen Gewinn der Toys&Joys Ges.m.b.H. optimiert.
Mathematischen Formulierung:
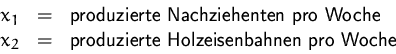

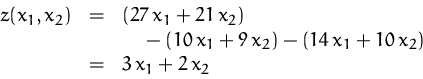
Müssen aber Nebenbedingungen beachten:
| Lackieren: | |
| Montage: | |
| Verkaufsbeschränkung: | |
| keine negativen Güter: |
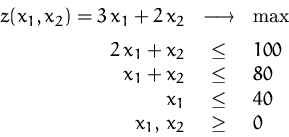
Die zu optimierende Funktion ![]() heißt die Zielfunktion
des linearen Optimierensproblems, die Ungleichungen die
Nebenbedingungen.
heißt die Zielfunktion
des linearen Optimierensproblems, die Ungleichungen die
Nebenbedingungen.