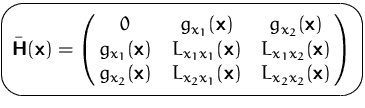
Zur Untersuchung der stationären Punkte können wir die geränderte Hesse-Matrix verwenden.
Sie lautet für Funktionen in zwei Variablen und einer Nebenbedingung
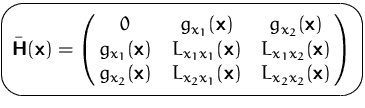
Ein stationärer Punkt ![]() von
von ![]() unter der Bedingung
unter der Bedingung
![]() ist ein
ist ein
BEISPIEL
Wir suchen die lokalen Extrema von
![]()
![]()
Der einzige stationäre Punkt von ![]() unter der Nebenbedingung
unter der Nebenbedingung ![]() ist
ist ![]() .
.
Die geränderte Hesse-Matrix an der Stelle ![]() lautet
lautet
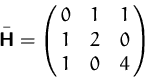
![]()
![]()
![]() ist ein lokales Minimum von
ist ein lokales Minimum von ![]() unter
der Nebenbedingung.
unter
der Nebenbedingung.