




previous: Der allgemeine Fall
up: Die Lagrange-Funktion
next: Die geränderte Hesse-Matrix
Fassen wir die Lagrange-Funktion
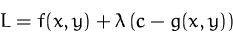
als Funktion von 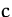 auf, und differenzieren nach
auf, und differenzieren nach 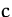 :
:
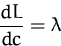
Im Optimum ist aber
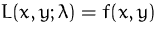 .
.
Der Lagrange-Multiplikator gibt also an, wie sich das Optimum ändert,
wenn die Konstante 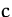 der Nebenbedingung
der Nebenbedingung
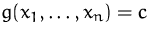 verändert wird.
verändert wird.





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![]()
![]()
![]() der Nebenbedingung
der Nebenbedingung
![]() verändert wird.
verändert wird.