




previous: Der zweidimensionale Fall
up: Die Lagrange-Funktion
next: Interpretation des Lagrange-Multiplikators
![\begin{displaymath}
\begin{array}
{rl}
\mbox{Max/Min} & f(x_1,\ldots,x_n) \\ [1...
...box[5em]{\dotfill} \\ & g_k(x_1,\ldots,x_n) = c_k
\end{array}\end{displaymath}](img1381.gif)
- (1)
- Aufstellen der Lagrange-Funktion
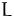 .
.
- (2)
- Berechnung die ersten partiellen Ableitungen von
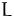 .
.
- (3)
- Setzen alle ersten partiellen Ableitungen gleich Null und
lösen das so entstandene Gleichungssystem mit
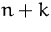 Unbekannten in
Unbekannten in
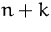 Gleichungen.
Gleichungen.
- (4)
- die ersten
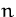 Komponenten
Komponenten 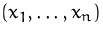 sind die
Koordinaten der gesuchten stationäre Punkte.
sind die
Koordinaten der gesuchten stationäre Punkte.
BEISPIEL
Wir suchen die stationären Punkte von
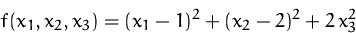
unter den Nebenbedingungen
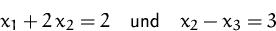
Die Lagrange-Funktion lautet:
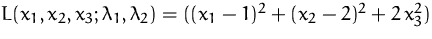
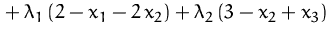
Die stationären Punkte von 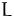 erhalten wir durch Nullsetzen der
ersten partiellen Ableitungen:
erhalten wir durch Nullsetzen der
ersten partiellen Ableitungen:
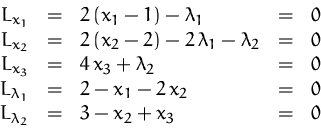
Dieses (lineare) Gleichungssystem hat die Lösung:
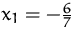 ,
, 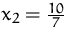 ,
, 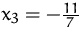 ;
; 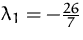 ,
, 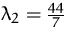 .
.
Der einzige stationäre Punkt von 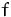 unter den Nebenbedingungen
ist somit
unter den Nebenbedingungen
ist somit 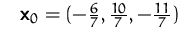 .
.





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![\begin{displaymath}
\begin{array}
{rl}
\mbox{Max/Min} & f(x_1,\ldots,x_n) \\ [1...
...box[5em]{\dotfill} \\ & g_k(x_1,\ldots,x_n) = c_k
\end{array}\end{displaymath}](img1381.gif)
![\begin{displaymath}
\begin{array}
{rl}
\mbox{Max/Min} & f(x_1,\ldots,x_n) \\ [1...
...box[5em]{\dotfill} \\ & g_k(x_1,\ldots,x_n) = c_k
\end{array}\end{displaymath}](img1381.gif)
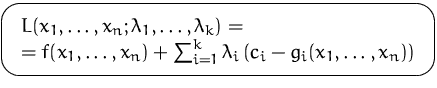
![]()
![]()
![]()
![]()
![]() erhalten wir durch Nullsetzen der
ersten partiellen Ableitungen:
erhalten wir durch Nullsetzen der
ersten partiellen Ableitungen:
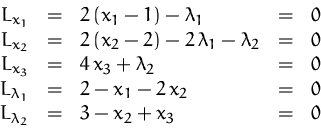
![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.![]() unter den Nebenbedingungen
ist somit
unter den Nebenbedingungen
ist somit ![]() .
.