previous: Die Elastizität up: Differentialrechnung next: Lokale und globale Extremwerte

Monotonie und Konvexität

DEFINITION (MONOTONIE)
Eine Funktion heißt monoton steigend in einem Intervall $[\,a,b\,]$ , falls für alle $x_1,x_2\in [\,a,b\,]$ gilt

$\begin{displaymath} x_1 \geq x_2\;\Leftrightarrow\;f(x_1)\geq f(x_2). \end{displaymath}$

Sie heißt monoton fallend, falls
$\begin{displaymath} x_1 \geq x_2\;\Leftrightarrow\;f(x_1)\leq f(x_2). \end{displaymath}$

$\begin{figure} \setlength {\unitlength}{1mm} \begin{picture} (125,55) \thinl... ...igend}} \put(100,0){\makebox(0,0)[t]{monoton fallend}}\end{picture}\end{figure}$

DEFINITION (KRüMMUNG)
Eine Funktion heißt konvex in einem Intervall $[\,a,b\,]$ , falls der Graph der Funktion immer unter der Sekante (oder Sehne) liegt, in Formeln:

falls für alle $x_1,x_2\in [\,a,b\,]$ und für alle $h\in[\,0,1\,]$

$\begin{displaymath} f(h\,x_1+(1-h)\,x_2)\leq h\,f(x_1)+(1-h)\,f(x_2). \end{displaymath}$

Die Funktion heißt konkav, falls
$\begin{displaymath} f(h\,x_1+(1-h)\,x_2)\geq h\,f(x_1)+(1-h)\,f(x_2). \end{displaymath}$

$\begin{figure} \setlength {\unitlength}{1mm} \begin{picture} (125,55) \thinl... ...ector(-1,1){4}} \put(94,19){\makebox(0,0)[l]{Sekante}}\end{picture}\end{figure}$

Für differenzierbare Funktionen erhalten wir folgende Kriterien für die Monotonie bzw. Krümmung von Funktionen:

$\mbox{\ovalbox{$\begin{Beqnarray*} f\mbox{ monoton steigend }&\Leftrightarrow& ... ... 0\\ f\mbox{ monoton fallend }&\Leftrightarrow& f'(x)\leq 0\end{Beqnarray*}$}}$

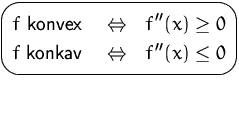
$\mbox{\ovalbox{$\begin{Beqnarray*} f\mbox{ konvex }&\Leftrightarrow& f''(x)\geq 0\\ f\mbox{ konkav }&\Leftrightarrow& f''(x)\leq 0\end{Beqnarray*}$}}$

Es gibt auch den Begriff streng monoton steigend, der definiert ist durch $x_1 \gt x_2\;\Leftrightarrow\;f(x_1)\gt f(x_2)$ . Nach unserer Definition ist die Funktion $f\colon x\mapsto 1$ monoton steigend, da immer $1\geq 1$ gilt, aber nicht streng monoton steigend, da $1\not\gt 1$ .

BEISPIEL
In welchem Bereich ist

$f(x)=2\,x^3-12\,x^2+18\,x-1$

monoton steigend?

Suchen den Bereich, wo $f'(x)\geq 0$ .

1.
$f'(x)= 6\,x^2-24\,x+18$

2.
Nullstellen:
$x^2-4\,x+3=0\quad\Rightarrow\quad x_1=1,\;x_2=3$

3.
Erhalte 3 Intervalle: $(\,-\infty,1\,]$ , $[\,1,3\,]$ und $[\,3,\infty\,)$

4.
Wähle ``geeigneten'' Punkt in jedem Intervall und bestimme dort das Vorzeichen von : $f'(0)=3 \gt 0$ , und $f'(4)=3 \gt$ .

5.
kann innerhalb eines Intervalls das Vorzeichen nicht ändern: $f'(x)\geq 0$ in $(\,-\infty,1\,]$ und $[\,3,\infty\,)$ .

Die Funktion ist monoton steigend in
$(\,-\infty,1\,]\cup [\,3,\infty\,)$ .