In allen Punkten, in denen sich keine Tangenten an den Graphen einer Funktion
In allen Punkten, in denen sich keine Tangenten an den Graphen
einer Funktion ![]() legen lassen, ist
legen lassen, ist ![]() nicht differenzierbar. Das
sind vor allem
nicht differenzierbar. Das
sind vor allem
BEISPIEL
Die Funktion
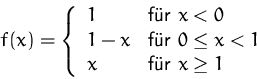
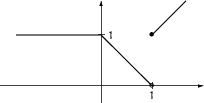
In 0 besitzt der Graph einen ,,Knick``, in 1 ist die Funktion nicht stetig.