




previous: Die Idee
up: Determinanten
next: Berechnung der Determinante
Wir fassen die Vektoren
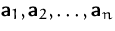 als Spaltenvektoren einer
als Spaltenvektoren einer 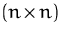 -Matrix
-Matrix
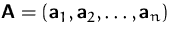 auf.
auf.
DEFINITION (DETERMINANTE)
Die Determinante ist eine Funktion, die jeder
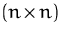 -Matrix
-Matrix 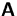 eine reelle Zahl
eine reelle Zahl
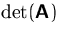 zuordnet und die folgenden Eigenschaften besitzt:
zuordnet und die folgenden Eigenschaften besitzt:
- (1)
- die
Determinante ist linear in jeder Spalte
(a) 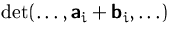
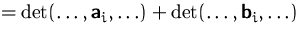
(b) 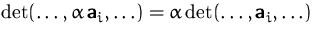
- (2)
- die
Determinante ist Null, falls zwei Spaltenvektoren gleich
sind
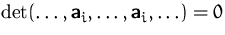
- (3)
- die Determinante ist normiert
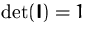
Andere Schreibweise:
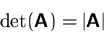
Die Eigenschaften (1) - (3) definieren eindeutig eine Funktion.
Diese Funktion besitzt noch eine Reihe weiterer Eigenschaften, die
sich aus diesen drei Grundeigenschaften herleiten lassen.
- (1)
- (2)
- (3)
-
- (4)
- die
Determinante ist alternierend
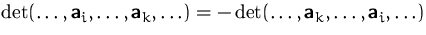
- (5)
- die
Determinante ist Null, falls ein Spaltenvektor der Nullvektor
ist
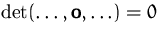
- (6)
- der
Wert der Determinante ändert sich nicht, wenn zu einer Spalte
das Vielfache einer anderen Spalte addiert wird
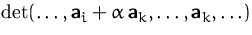
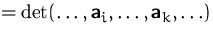
- (7)
- die Spaltenvektoren von
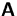 sind genau dann linear abhängig,
falls
sind genau dann linear abhängig,
falls 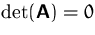
- (8)
- die Matrix
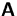 ist genau dann invertierbar, falls
ist genau dann invertierbar, falls
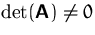
- (9)
- die
Determinante einer Dreiecksmatrix ist das Produkt der
Diagonalelemente

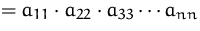
- (10)
- beim Transponieren ändert sich der Wert der Determinante nicht,
d.h. die Aussagen über Spalten gelten analog für Zeilen
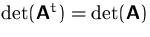
- (11)
- die Determinante des Produktes zweier Matrizen ist gleich dem
Produkt der Determinanten
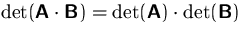
- (12)
- die Determinante der inversen Matrix ist gleich dem Kehrwert der
Determinante
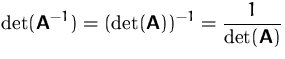
BEISPIEL
ad (1a)
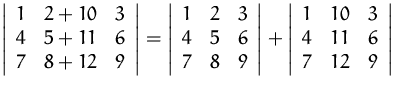
ad (1b)
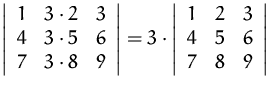
ad (2)
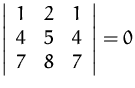
ad (4)
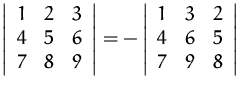
ad (6)
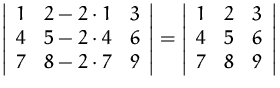
Einige Eigenschaften lassen sich leicht herleiten.
(1) + (2) 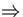 (4):
(4):
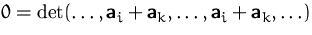
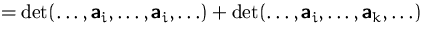
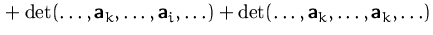
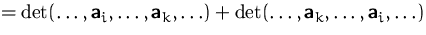
(1) + (2) 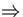 (5):
(5):
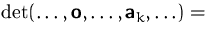
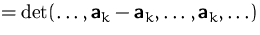
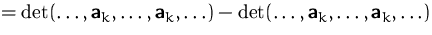
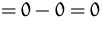
(1) + (2) 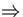 (6):
(6):
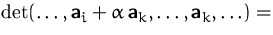
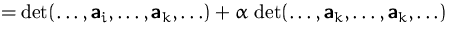
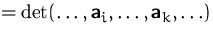





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![]() als Spaltenvektoren einer
als Spaltenvektoren einer ![]() -Matrix
-Matrix
![]() auf.
auf.
![]() -Matrix
-Matrix ![]() eine reelle Zahl
eine reelle Zahl
![]() zuordnet und die folgenden Eigenschaften besitzt:
zuordnet und die folgenden Eigenschaften besitzt:
![]()

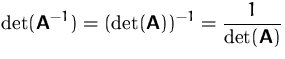
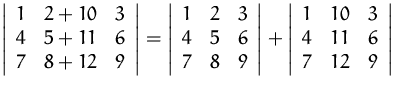
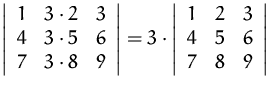
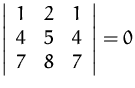
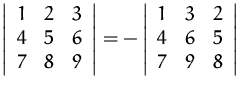
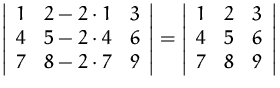
![]() (4):
(4):
![]()
![]()
![]()
![]()
![]() (5):
(5):
![]()
![]()
![]()
![]()
![]() (6):
(6):
![]()
![]()
![]()