Zwei Vektoren im
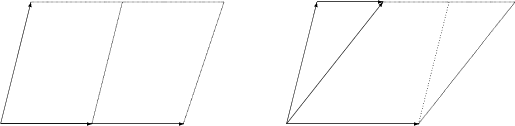
Zwei Vektoren im ![]() spannen ein Parallelogramm auf.
spannen ein Parallelogramm auf.
Stehen die beiden Vektoren normal aufeinander, so ist der Flächeninhalt groß. Sind die beiden Vektoren linear abhängig, so ist der Flächeninhalt gleich Null.

Wir verwenden das ![]() -dimensionale Volumen für unsere Funktion zum
,,Messen`` der linearen Abhängigkeit.
-dimensionale Volumen für unsere Funktion zum
,,Messen`` der linearen Abhängigkeit.
Wir definieren diese Funktion indirekt durch die Eigenschaften, die wir von einem Volumen verlangen.
Für das Volumen gilt:
Wir bezeichnen diese Funktion als Determinante.