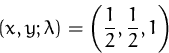Wir untersuchen zuerst die Auswirkung der Nichtnegativitätsbedingung
auf das Maximum einer Funktion in einer Variablen.
Für ein (lokales) Maximum ![]() gibt es drei Möglichkeiten
gibt es drei Möglichkeiten
Zusammengefaßt:
![]()
![\begin{figure}
\setlength {\unitlength}{1.5mm}
\begin{tabular}[t]
{ccccc}
\be...
... \spline(5,22)(10,15)(15,12)(20,11)(25,10)\end{picture}\end{tabular}\end{figure}](img1571.gif)
Im Falle einer Funktion ![]() in mehreren Variablen erhalten
wir für jede Variable
in mehreren Variablen erhalten
wir für jede Variable ![]() so eine Bedingung:
so eine Bedingung:
![]()
Wir können die Nebenbedingungen unseres usprünglichen Problems durch Einfügen von Schlupfvariablen in ein System von Gleichungen mit Nichtnegativitätsbedingung überführen (vgl. Simplex-Algorithmus).
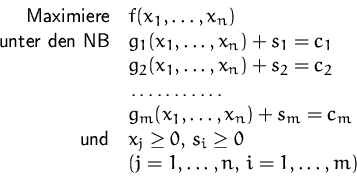
Verwenden wieder die Lagrange-Funktion:
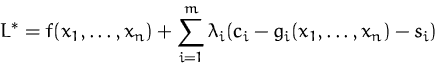
Berücksichtigen der Nichtnegativitätsbedingung:
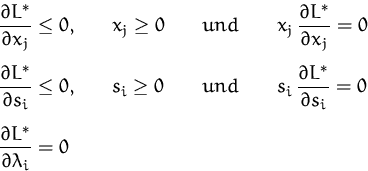
Die Schlupfvariablen lassen sich wieder eliminieren:
Wegen ![]() ,
wird zweite Zeile zu
,
wird zweite Zeile zu
![]()
![]()
![]()
Jetzt brauchen wir die Schlupfvariablen nicht mehr.
Verwenden statt ![]() direkt die Lagrange-Funktion
direkt die Lagrange-Funktion
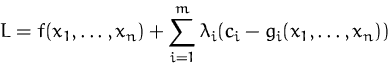
Wegen
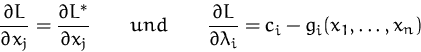

Dieses Kriterium für das lokale Maximum einer Funktion unter
Nebenbedingungen heißt Kuhn-Tucker Bedingung.
BEISPIEL
Wir suchen das Maximum von
![]()
![]()
Durch die Lagrange-Funktion
![]()
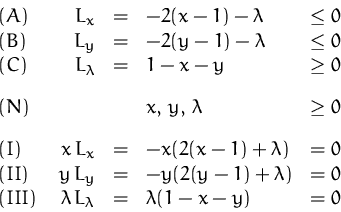
Schreiben ![]() -
-![]() an als
an als
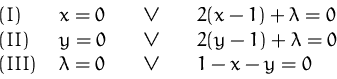
![]() ,
, ![]() ,
, ![]() und
und ![]() .
.
Keiner dieser Fälle erfüllt alle
Nebenbedingungen ![]() ,
, ![]() und
und ![]() .
.
![]() .
.
Wir erhalten daher durch
![]() :
: ![]() .
.
Zusammen mit ![]() erhalten wir daraus
erhalten wir daraus
![]() und aus
und aus ![]() ,
, ![]() .
.
Die Kuhn-Tucker-Bedingung wird daher nur vom Punkt