previous: Kuhn-Tucker up: Kuhn-Tucker next: Die Kuhn-Tucker Bedingung

Eine graphische Methode  

Im Falle zweier Variablen (vgl. lineare Optimierung).

(1)

Wir zeichnen den zulässigen Bereich als Schnittmenge der Mengen, die durch die Nebenbedigungen 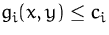$g_i(x,y)\leq c_i$ beschrieben werden, in der 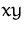$xy$-Ebene ein.

(2)

Wir zeichnen ,,geeignete`` Isoquanten (Niveaulinien) der zu optimierenden Funktion 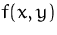$f(x,y)$ ein.

(3)

Wir interpretieren die Zeichnung und suchen einen Punkt mit größten Funktionswert von 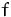$f$, der im zulässigen Bereich liegt.

BEISPIEL
Das Maximum von 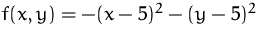$f(x,y)=-(x-5)^2-(y-5)^2$ unter den Nebenbedingungen

$$x^2+y\leq 9,\qquad x+y\leq 8,\qquad x,y\geq 0$$

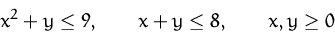
liegt am Rand des zulässigen Bereichs (ungefähr) im Punkt $(2{,}1;4{,}3)$.

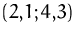(siehe Abbildung, oben. Der Funktionswert von 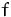$f$ wird umso kleiner, je größer der Durchmesser der Niveaulinie ist. Der zulässige Bereich ist schattiert.)

BEISPIEL
Das Maximum von 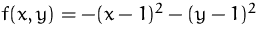$f(x,y)=-(x-1)^2-(y-1)^2$ unter den Nebenbedingungen

$$x^2+y\leq 9,\qquad x+y\leq 8,\qquad x,y\geq 0$$

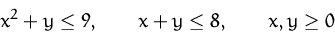
liegt im Inneren des zulässigen Bereichs im Punkt 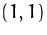$(1,1)$.

(siehe Abbildung, unten).