




previous: Das Standard-Minimierungsproblem
up: Lineare Optimierung
next: Spezialfälle
![\begin{displaymath}
\begin{array}
{rcl}
z(x_1,x_2)=11\,x_1+8\,x_2 &\longrightar...
... + 4\,x_2 &\leq& 60\\ [0.5ex]
x_1,\,x_2 &\geq& 0\\ \end{array}\end{displaymath}](img1501.gif)
Aus dem Anfangs-Simplex-Tableau
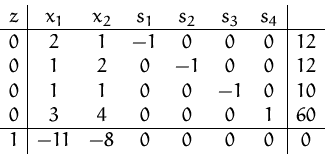
erhalten wir die nicht zulässige Basislösung
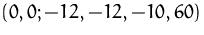 .
.
 2-Phasen-Simplex-Algorithmus
2-Phasen-Simplex-Algorithmus
- 1. Phase:
- Suchen zulässige Basislösung mit Hilfe des
Simplex-Algorithmus und einer Hilfszielfunktion.
- 2. Phase:
- Berechnen des Optimums mit Hilfe des
Standard-Verfahrens.
1. Phase:
Die Suche nach einem Startpunkt
- (1)
- Aufstellen des Anfangs-Simplex-Tableaus.
In jeder Zeile, in der wir eine Schlupfvariable
subtrahieren, addieren wir zusätzlich eine
Hilfsvariable 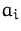 .
.
- (2)
- Ersetzen die Zielfunktion durch die Summe aller Hilfsvariablen
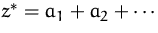 .
.
- (3)
- Durch Addition aller Zeilen, die eine Hilfsvariable enthalten, zur
Zielfunktionszeile bringen wir alle Einträge der Hilfsvariablen
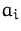 in der Zielfunktionszeile auf Null.
in der Zielfunktionszeile auf Null.
- (4)
- Minimieren diese Hilfszielfunktion
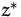 mit dem
Standardverfahren.
mit dem
Standardverfahren.
- (5)
- Im Minimum von
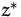 gibt es drei Möglichkeiten:
gibt es drei Möglichkeiten:
- (a)
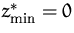 und keine Hilfsvariable ist Basisvariable
und keine Hilfsvariable ist Basisvariable
- gehe zu Punkt (6).
- (b)
 und eine Hilfsvariable ist Basisvariable
und eine Hilfsvariable ist Basisvariable
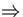
- Durch geeignete Pivotschritte, die
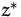 unverändert
lassen, können alle Hilfsvariablen zu Nichtbasisvariablen
gemacht werden.
unverändert
lassen, können alle Hilfsvariablen zu Nichtbasisvariablen
gemacht werden.
Anschließend gehe zu Punkt (6).
- (c)
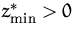
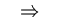 zulässiger Bereich
zulässiger Bereich

- (6)
- Streiche die Spalten der Hilfsvariablen aus dem Tableau und setze
wieder die ursprüngliche Zielfunktion
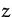 ein.
ein.
- (7)
- Durch Addition eines Vielfachen von geeigneten Zeilen zur
Zielfunktionszeile bringen wir alle Einträge der Basisvariablen
in der Zielfunktionszeile auf Null.
2. Phase:
Lösen des Optimierungsproblems
- (8)
- Löse das lineare Optimierungsproblem mit dem
Standardverfahren.
BEISPIEL FORTSETZUNG
1. Phase:

Wenn wir 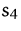 ,
, 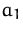 ,
, 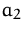 und
und  als
Basisvariable wählen, erhalten wir die zulässige Basislösung
als
Basisvariable wählen, erhalten wir die zulässige Basislösung
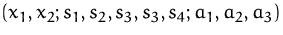
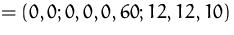
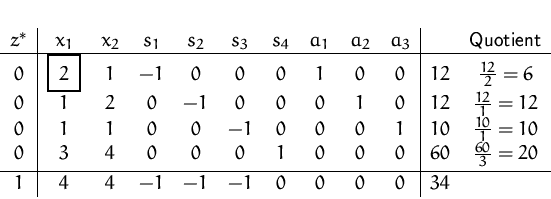
Minimieren der Hilfszielfunktion:

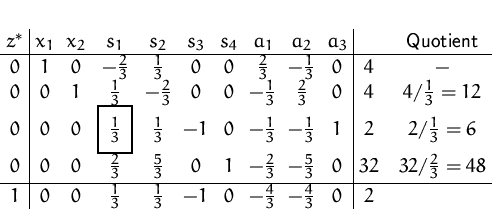

Wir haben 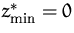 erreicht, und die drei
Hilfsvariablen
erreicht, und die drei
Hilfsvariablen 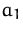 ,
, 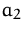 und
und 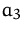 sind keine Basisvariablen mehr.
sind keine Basisvariablen mehr.
Die (zulässige) Basislösung lautet
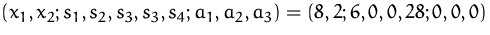 .
.
2. Phase:
Wir setzen jetzt wieder die ursprüngliche Zielfunktion in unser
Tableau ein:
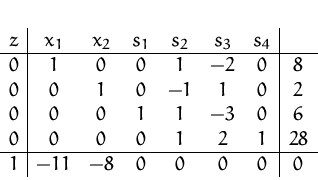
Wir müssen die ZFZ umformen, da 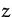 durch die zwei Basisvariablen
durch die zwei Basisvariablen
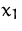 und
und 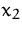 ausgedrückt wird.
ausgedrückt wird.
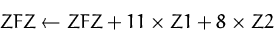
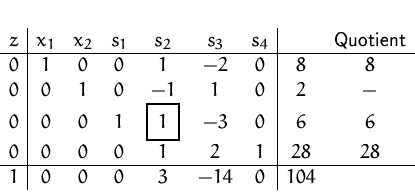
Können nun das Minimierungsproblem mit dem
Standardverfahren
lösen:

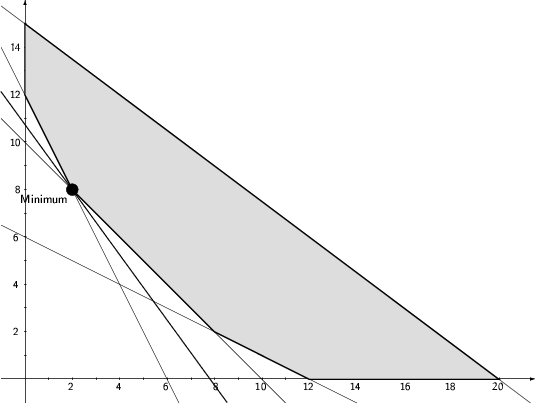
Die optimale zulässige Basislösung ist
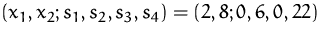 ,
,
d.h. das Minimum liegt im Punkt 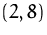 . Der minimale Zielfunktionswert
ist
. Der minimale Zielfunktionswert
ist 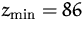 .
.





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![\begin{displaymath}
\begin{array}
{rcl}
z(x_1,x_2)=11\,x_1+8\,x_2 &\longrightar...
... + 4\,x_2 &\leq& 60\\ [0.5ex]
x_1,\,x_2 &\geq& 0\\ \end{array}\end{displaymath}](img1501.gif)
![\begin{displaymath}
\begin{array}
{rcl}
z(x_1,x_2)=11\,x_1+8\,x_2 &\longrightar...
... + 4\,x_2 &\leq& 60\\ [0.5ex]
x_1,\,x_2 &\geq& 0\\ \end{array}\end{displaymath}](img1501.gif)
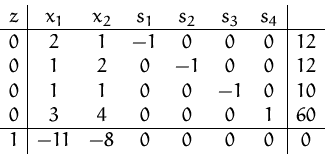
![]() 2-Phasen-Simplex-Algorithmus
2-Phasen-Simplex-Algorithmus

![]() ,
, ![]() ,
, ![]() und
und ![]() als
Basisvariable wählen, erhalten wir die zulässige Basislösung
als
Basisvariable wählen, erhalten wir die zulässige Basislösung
![]()
![]()
![]()




![]() erreicht, und die drei
Hilfsvariablen
erreicht, und die drei
Hilfsvariablen ![]() ,
, ![]() und
und ![]() sind keine Basisvariablen mehr.
sind keine Basisvariablen mehr.
![]() .
.
![]() durch die zwei Basisvariablen
durch die zwei Basisvariablen
![]() und
und ![]() ausgedrückt wird.
ausgedrückt wird.
![]()


![]() ,
,![]() . Der minimale Zielfunktionswert
ist
. Der minimale Zielfunktionswert
ist ![]() .
.