previous: Der zulässige Bereich up: Der Simplex-Algorithmus next: Der Algorithmus

Naive Methode  

(1)

Berechne alle Basislösungen.

(2)

Überprüfe Nichtnegativitätsbedingung.

(3)

Berechne Zielfunktion.

(4)

Suche Maximum.

Im Falle von $n$ Variablen $x_j$ und $m$ Ungleichungen gibt es allerdings nach den Gesetzen der Kombinatorik

$${n+m\choose n} = \frac{(n+m)!}{m!\,n!}$$

viele Basislösungen.

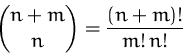
Für jede Basislösung muß ein lineares Gleichungssystem mit $m$ Unbekannten gelöst werden.

z.B.: 9 Variable, 12 Ungleichungen

$\Rightarrow\quad {21\choose 9} = 293\,930$ Basislösungen.

Die Methode ist daher für große lineare Optimierungsprobleme nicht geeignet.