




previous: Lagrange-Multiplikatoren
up: Lagrange-Multiplikatoren
next: Die Lagrange-Funktion
Wir suchen die lokalen Extrema einer Funktion 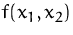 unter
der Bedingung, daß
unter
der Bedingung, daß 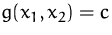 .
.
- (1)
- Wir zeichnen die Nebenbedingung
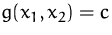 in der
in der
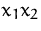 -Ebene ein.
-Ebene ein.
- (2)
- Wir zeichnen ,,geeignete`` Isoquanten
(Niveaulinien) der zu
optimierenden Funktion
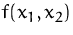 ein.
ein.
- (3)
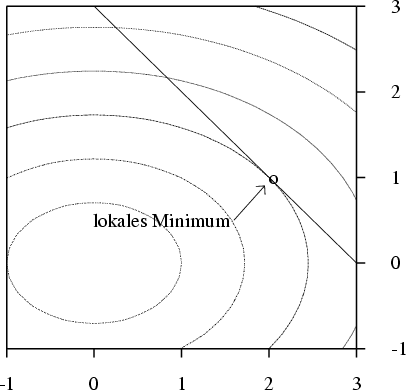
- Wir untersuchen an Hand der Zeichnung, welche Isoquanten von der
Nebenbedingung geschitten werden und bestimmen so die ungefähre Lage
des Optimums.
BEISPIEL
Wir suchen die lokalen Extrema von
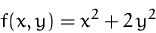
unter der Nebenbedingung
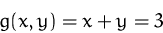





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![]() unter
der Bedingung, daß
unter
der Bedingung, daß ![]() .
.![]()
![]()