Eine reelle Funktion in mehreren Variablen ist eine Abbildung, die jedem Vektor
DEFINITION ()
Eine reelle Funktion in mehreren Variablen ist eine
Abbildung, die jedem Vektor ![]() eine reelle Zahl zuordnet.
eine reelle Zahl zuordnet.
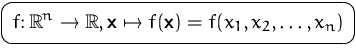
Die Komponenten ![]() des Vektors
des Vektors ![]() heißen die
Variablen der Funktion
heißen die
Variablen der Funktion ![]() .
.
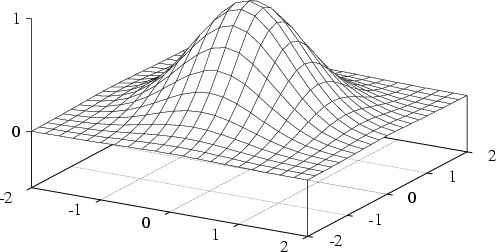
Funktionen in zwei Variablen lassen sich durch den Graphen (oder Funktionengebirge) veranschaulichen.
Dabei wird für jeden Punkt in der ![]() -Ebene der Funktionswert
-Ebene der Funktionswert
![]() in die
in die ![]() -Richtung eingezeichnet
(vgl.).
-Richtung eingezeichnet
(vgl.).
BEISPIEL
![]() ist eine Funktion in zwei Variablen.
ist eine Funktion in zwei Variablen.
Eine Isoquante (oder Höhenlinie,
Niveaulinie) ist die Menge aller Punkte ![]() mit
mit ![]() (
(![]() ).
Die Funktion
).
Die Funktion ![]() hat daher auf einer Höhenlinie den
gleichen Funktionswert.
Höhenlinien sind eine weitere Möglichkeit
Funktionen in zwei Variablen graphisch darzustellen.
hat daher auf einer Höhenlinie den
gleichen Funktionswert.
Höhenlinien sind eine weitere Möglichkeit
Funktionen in zwei Variablen graphisch darzustellen.
![\begin{figure}
\mbox{}\\ [-13ex]
\hbox{\epsfxsize=11cm\epsfbox{figures/Funktione...
...=11cm\epsfbox{figures/Funktionen2_Contour.2.eps}}
\\ [-12ex]\mbox{}
\end{figure}](img1202.gif)