Eine Teilmenge
DEFINITION (KONVEXE MENGE)
Eine Teilmenge ![]() des
des ![]() heißt
konvex, wenn für
zwei beliebige Punkte
heißt
konvex, wenn für
zwei beliebige Punkte ![]() auch die Verbindungsstrecke dieser
Punkten Punkte in
auch die Verbindungsstrecke dieser
Punkten Punkte in ![]() liegt. d.h.
liegt. d.h.
![]()
für alle ![]() , und
, und ![]()
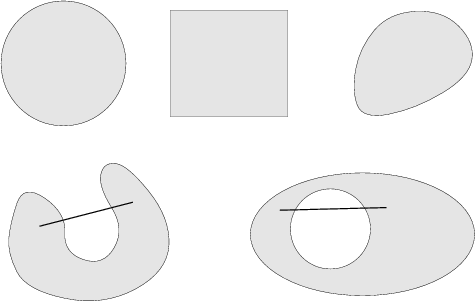
Nur die Mengen in der ersten Reihe sind konvex.