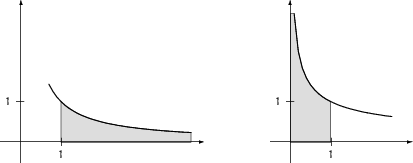
sind Integrale, bei denen

Das Integral wird mit Hilfe eines Grenzwertes berechnet.
Z.B. falls ![]() in
in ![]() nicht definiert ist, oder
nicht definiert ist, oder ![]() :
:
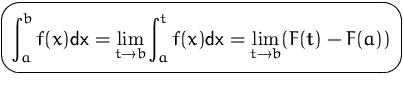
BEISPIEL
Die Funktion ![]() ist in
ist in ![]() nicht
definiert.
nicht
definiert.
Fassen 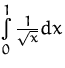 als Abkürzung
für
als Abkürzung
für ![]() auf.
auf.
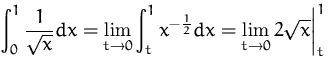
![]()
BEISPIEL
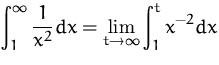
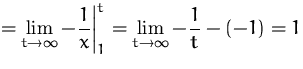
BEISPIEL
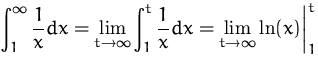
![]()
Das uneigentliche Integral existiert somit nicht.