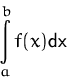
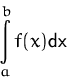
Berechnung durch Approximation von ![]() durch
Treppenfunktionen:
durch
Treppenfunktionen:
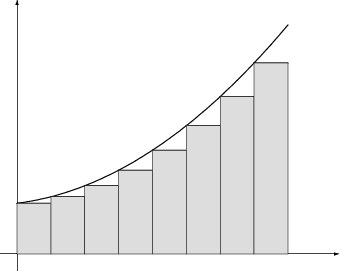
Einfacher für stetige Funktionen
( Hauptsatzes der Differential- und Integralrechnung):
Sei ![]() eine Stammfunktion von
eine Stammfunktion von ![]() ,dann gilt für das Integral
,dann gilt für das Integral
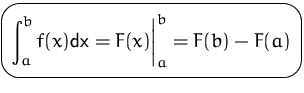
BEISPIEL
Wir suchen das Integral der Funktion
![]() im Intervall
im Intervall ![]() .
.
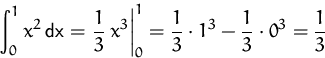
Erklärung des Hauptsatzes:
Wir bezeichnen mit ![]() die Fläche zwischen dem Graphen einer
Funktion
die Fläche zwischen dem Graphen einer
Funktion ![]() und der
und der ![]() -Achse zwischen 0 und
-Achse zwischen 0 und ![]() .
.
![\begin{figure}
\setlength {\unitlength}{1.2mm}
\begin{picture}
(100,80)
\line...
...l]{\footnotesize $M_h=\max\limits_{t\in[x,x+h]} f(t)$}}\end{picture}\end{figure}](img1165.gif)
![]()
![]()
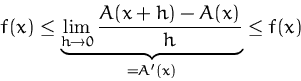
![]()