previous: Matrizen und Vektoren up: Matrizen und Vektoren next: Spezielle Matrizen

Was sind Matrizen?  

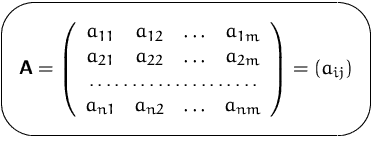
Wir haben die Koeffizienten des linearen Gleichungssystems in ein rechteckiges Schema geschrieben:

$\mbox{\ovalbox{$\displaystyle \mathsfbf{A}= \left( \begin{array} {cccc} a_{1... ...{c}\dotfill\\ a_{n1}&a_{n2}&\ldots&a_{nm}\\ \end{array} \right)= (a_{ij})$}}$

Ein solches Schema mit $n$ Zeilen und $m$ Spalten -- eingeschlossen in (ev. rechteckigen) Klammern -- heißt $n\times m$- Matrix, und wird mit Großbuchstaben bezeichnet.

Die Zahlen $a_{ij}$ heißen  Elemente oder Koeffizienten der Matrix $\mathsfbf{A}$,die Zahl $i$ der  Zeilenindex, die Zahl $j$ der  Spaltenindex.

Der Koeffizient $a_{ij}$ ist also die Zahl in der $i$-ten Zeile und $j$-ten Spalte (Zeilenindex vor Spaltenindex) von $\mathsfbf{A}$.