

previous: 28. Jänner 1997
next: 1. Oktober 1996
Gegeben sei
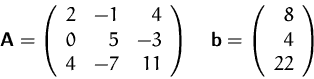
- (a)
- Bestimmen Sie den Rang der Matrix
 .
. - (b)
- Wieviele Lösungen besitzt das Gleichungssystem
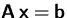 ?
?
- (c)
- Berechnen Sie die Determinante von
 .
. - (d)
- Ist
 invertierbar? (Begründung)
invertierbar? (Begründung)
- (e)
- Sind die Zeilenvektoren untereinander linear unabhängig?
(Lösung)
Lösen Sie die Matrizengleichung nach 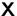 auf
auf
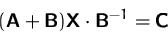
(Lösung)
Berechnen Sie 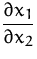 aus
der impliziten Funktion
aus
der impliziten Funktion
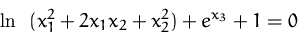
(Lösung)
- (a)
- Bestimmen Sie die Elastizität von

- (b)
- Bestimmen Sie die Bereiche in denen
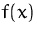 elastisch,
unelastisch bzw. 1-elastisch ist.
elastisch,
unelastisch bzw. 1-elastisch ist.
(Lösung)
Lösen Sie das Optimierungsproblem
Max/Min
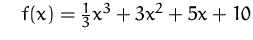
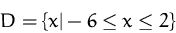
(Lösung)
- (a)
- Berechnen Sie die Determinante von
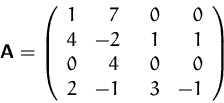
- (b)
- Berechnen Sie die Determiante von
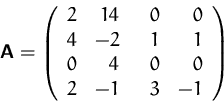
- (c)
- Berechnen Sie die Determinante von
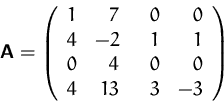
(Lösung)
- (a)
- Bestimmen Sie stationären Punkte der Funktion
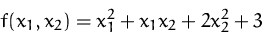
unter der Nebenbedingung
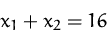
mittels Lagrange-Multiplikatoren.
- (b)
- Handelt es sich um einen globalen Extremwert?
(Lösung)
Bestimmen Sie die stationären Punkte der Funktion
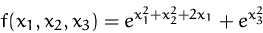
(Lösung)
![\begin{displaymath}
\begin{array}
{rcl}
\mbox{Min/Max} && 3x_1 + x_2\\ [1ex]
\...
... x_2 &\le& 10 \\ x_2 &\le& 4 \\ x_1, x_2 &\ge& 0
\end{array}\end{displaymath}](img129.gif)
- (a)
- Lösen Sie das lineare Optimierungsproblem mit dem
Simplexalogorithmus.
- (b)
- Lösen Sie das Problem graphisch (Min,Max).
- (c)
- Zeichnen Sie die neue Lösung (Min, Max) ein, wenn
zusätzlich noch die Nebenbedingung
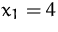 eingeführt
wird.
eingeführt
wird.
(Lösung)
Bestimmen Sie die Lösung des folgenden Gleichungssystems
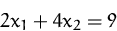
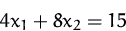
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
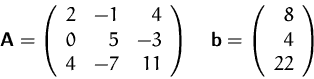
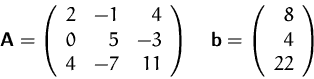
![]()
![]()
![]()
![]()
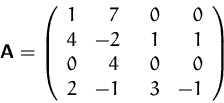
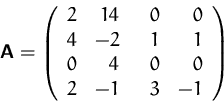
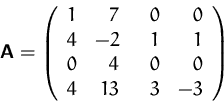
![]()
![]()
![]()
![\begin{displaymath}
\begin{array}
{rcl}
\mbox{Min/Max} && 3x_1 + x_2\\ [1ex]
\...
... x_2 &\le& 10 \\ x_2 &\le& 4 \\ x_1, x_2 &\ge& 0
\end{array}\end{displaymath}](img129.gif)
![]()
![]()
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)