

previous: 25. Februar 1997
next: 20. November 1996
Berechnen Sie die Ableitung 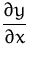 der impliziten Funktion
der impliziten Funktion
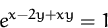
(Lösung)
Bestimmen Sie die Bereiche, in denen die Funktion 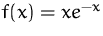 elastisch, unelastisch bzw. 1-elastisch ist.
elastisch, unelastisch bzw. 1-elastisch ist.
(Lösung)
Bestimmen Sie das globale Maximum und Minimum der Funktion
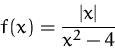
auf dem Intervall ![$[-1,1]$](img102.gif) .
.(Lösung)
Berechnen Sie die Lösung(en) des linearen Gleichungssystem
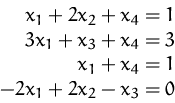
(Lösung)
- (a)
- Berechnen Sie die Determinante der Matrix
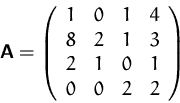
- (b)
- Berechnen Sie die Determinante von
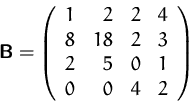
mit Hilfe der Determinate von  , indem Sie die Rechenregeln über
Zeilen- und Spaltentransformationen anwenden.
, indem Sie die Rechenregeln über
Zeilen- und Spaltentransformationen anwenden.
(Lösung)
- (a)
- Bestimmen Sie stationären Punkte der Funktion
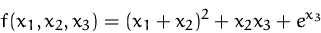
- (b)
- Untersuchen Sie mit Hilfe der Hessematrix, ob es sich bei
diesen Punkten um Maxima oder Minima handelt.
(Lösung)
Lösen Sie das folgende lineare Optimierungsproblem mit dem
Simplexalgorithmus
(Lösung)
Lösen Sie das folgende Optimierungsproblem für 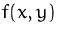 unter der Nebenbedingung
unter der Nebenbedingung 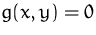 .
.
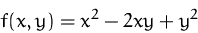
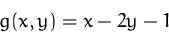
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
![]()
![]()
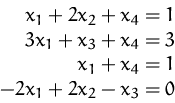
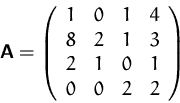
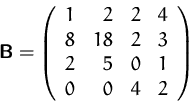
![]()
![]()
![]()
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)