

previous: 22. April 1997
next: 28. Jänner 1997
Bestimmen Sie die partielle Ableitung 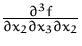 der Funktion
der Funktion
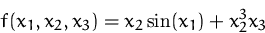
(Lösung)
Ein Unternehmen stellt drei Produkte, A, B und C her. Die Stückkosten für die
Herstellung sind  (A),
(A),  (B) und
(B) und 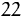 (C) Geldeinheiten, die entsprechenden
Verkaufspreise
(C) Geldeinheiten, die entsprechenden
Verkaufspreise 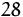 (A),
(A), 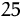 (B) und
(B) und 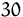 (C) Geldeinheiten. Alle nachfolgenden
Angaben beziehen sich auf den Planungshorizont der nächsten sechs Monate. Die am
Markt maximal absetzbare Stückzahl des Produkts A in dieser Zeit ist
(C) Geldeinheiten. Alle nachfolgenden
Angaben beziehen sich auf den Planungshorizont der nächsten sechs Monate. Die am
Markt maximal absetzbare Stückzahl des Produkts A in dieser Zeit ist 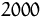 Einheiten. Aufgrund einer vertraglichen Verpflichtung müssen
Einheiten. Aufgrund einer vertraglichen Verpflichtung müssen 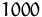 Einheiten des Produkts B und
Einheiten des Produkts B und 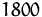 Einheiten des Produkts C gefertigt werden. Ein
weitergehender Absatz von B ist nicht möglich, bei C kann über diese Minimalmenge
hinaus noch mit einem Absatz von bis zu
Einheiten des Produkts C gefertigt werden. Ein
weitergehender Absatz von B ist nicht möglich, bei C kann über diese Minimalmenge
hinaus noch mit einem Absatz von bis zu 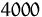 Einheiten am Markt gerechnet werden.
Einheiten am Markt gerechnet werden.
Die drei Produkte durchlaufen zwei Produktionsphasen. Die benötigte Anzahl von
Maschinenstunden für die Herstellung einer Einheit jedes der drei Produkte in jeder
der beiden Produktionsphasen ist in der nachfolgenden Tabelle dargestellt.
| |
Phase 1 |
Phase 2 |
| A |
0,6 |
0,7 |
| B |
0,8 |
1,1 |
| C |
0,9 |
0,5 |
In Produktionsphase 1 stehen maximal 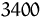 Maschinenstunden, in Phase 2
Maschinenstunden, in Phase 2 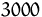 Maschinenstunden zur Verfügung.
Maschinenstunden zur Verfügung.
- (a)
- Geben Sie Zielfunktion und sämtliche Nebenbedingungen des linearen
Optimierungproblems an, mit dem der Produktionsplan des Unternehmens (die
herzustellende Stückzahl von A,B und C), der den Gewinn maximiert berechnet werden
kann.
- (b)
- Transformieren Sie das lineare Optimierungsproblem in die Standardform.
Hinweis: Die Lösung des Optimierungsproblems mit dem
Simplexalgorithmus ist nicht Teil der Aufgabenstellung.
(Lösung)
Bestimmen Sie, falls möglich, die Inverse der Matrix
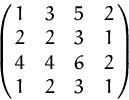
(Lösung)
Bestimmen Sie den Gradienten der Funktion
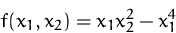
im Punkt 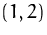 .
.(Lösung)
Bestimmen Sie die Lösungen des linearen Gleichungssystems
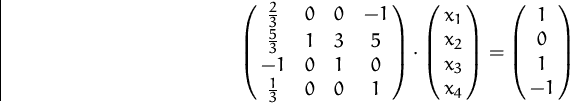
(Lösung)
- (a)
- Bestimmen Sie ein lokales Minimum der Funktion

Zeigen Sie die Minimumseigenschaft mit Hilfe der Hessematrix.
- (b)
- Hat die Funktion im gesamten Definitionsbereich ein einheitliches Krümmungsverhalten?
Untersuchen Sie diese Frage ebenfalls mit der Hessematrix und geben Sie an, ob es
sich beim zuvor gefundenen Minimum um ein globales Minimum
handelt.
(Lösung)
Bestimmen Sie den Rang der Matrix
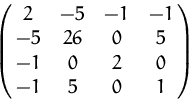
(Lösung)
Bestimmen Sie die Kofaktorenmatrix zu
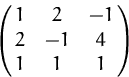
(Lösung)
Bestimmen Sie 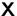 aus der Matrixgleichung
aus der Matrixgleichung
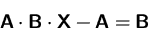
Gehen Sie davon aus, daß  und
und 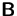 quadratische
Matrizen gleicher Größe wie
quadratische
Matrizen gleicher Größe wie 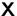 sind.
sind.
(Lösung)
Bestimmen Sie die stationären Punkte der Funktion
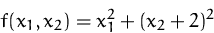
unter der Nebenbedingung 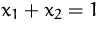 mit Hilfe von
Lagrangemultiplikatoren.
mit Hilfe von
Lagrangemultiplikatoren.
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
![]()
![]() Maschinenstunden, in Phase 2
Maschinenstunden, in Phase 2 ![]() Maschinenstunden zur Verfügung.
Maschinenstunden zur Verfügung.
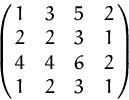
![]()
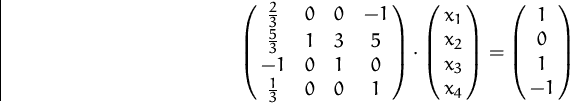
![]()
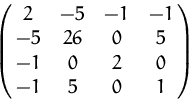
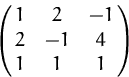
![]()
![]()
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)