

previous: 26. Juni 1997
next: 25. Februar 1997
Bestimmen Sie die Ableitung 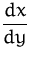 der
impliziten Funktion
der
impliziten Funktion
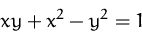
(Lösung)
Sei
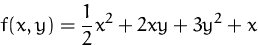
- (a)
- Berechnen Sie alle stationären Punkte von
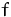 .
. - (b)
- Bestimmen Sie mit Hilfe der Hessematrix, ob es sich dabei um lokale
Minima, Maxima oder Sattelpunkte handelt.
- (c)
- Bestimmen Sie die Krümmung von
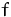 (konkav/konvex).
(konkav/konvex).
- (d)
- Gibt es globale Minima und Maxima? Welche?
(Lösung)
Berechnen Sie alle stationären Punkte von
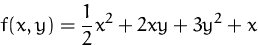
unter der Nebenbedingung
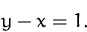
(Lösung)
Lösen sie die folgende Optimierungsaufgabe. (Gesucht sind alle
globalen Extrema.)
Min/Max
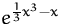
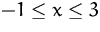
(Lösung)
Bestimmen Sie, falls möglich, die Inverse der Matrix
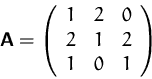
(Lösung)
Sei
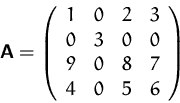
- (a)
- Berechnen Sie
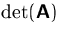 .
. - (b)
- Ist
 invertierbar?
invertierbar?
- (c)
- Ist
 singulär oder regulär?
singulär oder regulär?
- (d)
- Hat
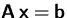 für
für
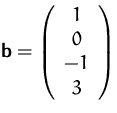 eine eindeutig bestimmte Lösung?
eine eindeutig bestimmte Lösung?
(Lösung)
Bestimmen Sie 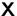 aus der Matrixgleichung
aus der Matrixgleichung
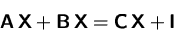
Gehen Sie davon aus, daß  ,
, 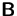 ,
, 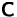 und
und 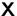 quadratische Matrizen gleicher Größe sind.
quadratische Matrizen gleicher Größe sind.
(Lösung)
Gegeben ist folgendes lineares Optimierungssystem
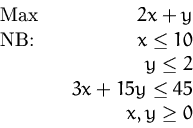
- (a)
- Lösen Sie das Optimierungsproblem graphisch.
- (b)
- Lösen Sie das Optimierungsproblem mit dem Simplexalgorithmus.
(Lösung)
- (a)
- Berechnen Sie die Elastizität von
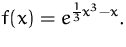
- (b)
- Ist
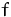 an der Stelle
an der Stelle 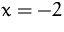 elastisch?
elastisch?
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
![]()
![]()
![]()
![]()
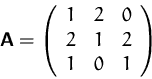
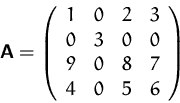
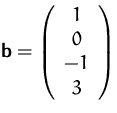 eine eindeutig bestimmte Lösung?
eine eindeutig bestimmte Lösung?
![]()
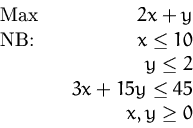
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)