

previous: 27. Jänner 1998
next: 26. Juni 1997
Berechnen Sie die Lösungen des linearen Gleichungssystems
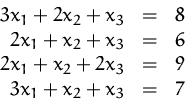
(Lösung)
Berechnen Sie die Lösung 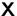 der Matrixgleichung
der Matrixgleichung
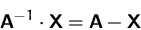
Gehen Sie davon aus, daß die diversen Matrixoperationen alle definiert
(Zeilen- bzw. Spaltenanzahl der Faktormatrizen, Invertierbarkeit) sind.
(Lösung)
Berechnen Sie 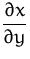 der
implizit gegebenen Funktion
der
implizit gegebenen Funktion
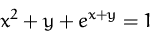
(Lösung)
Berechnen Sie das Ergebnis der Vereinfachung des Matrixausdrucks
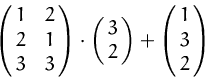
(Lösung)
Das folgende lineare Optimierungsproblem hat unendlich viele Maxima:
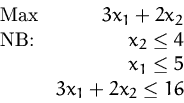
Zeigen Sie diese Eigenschaft
- (a)
- mit Hilfe der graphischen Lösung des Problems,
- (b)
- mit Hilfe der Lösung durch den Simplexalgorithmus.
Begründen Sie Ihre Lösung in beiden Fällen in Stichworten.
(Lösung)
Die Funktion
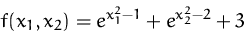
hat in 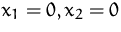 ein Minimum. Weisen Sie die
Minimumseigenschaft mit der Hessematrix nach.
ein Minimum. Weisen Sie die
Minimumseigenschaft mit der Hessematrix nach.
(Lösung)
Welches Krümmungsverhalten (konkav/konvex, Änderungen der Krümmung)
hat die Funktion
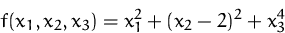
(Lösung)
Bestimmen Sie den Rang der Koeffizientenmatrix des Gleichungssystems
aus Beispiel 10.
(Lösung)
Bestimmen Sie die Kofaktoren der Matrix
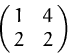
(Lösung)
Bestimmen Sie das totale Differential der Funktion
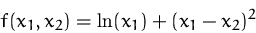
(Lösung)
Zeichnen Sie die Höhenlinie für 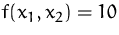 der Funktion
der Funktion
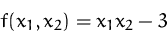


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
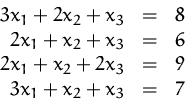
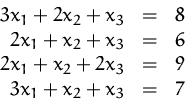
![]()
![]()
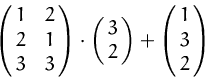
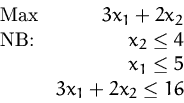
![]()
![]()
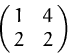
![]()
![]()
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)