

previous: Musterklausuren aus Mathematik I
next: 29. September 1997
- (a)
- Bestimmen Sie mit Hilfe des Rangs der Koeffizientenmatrix bzw. erweiterten
Koeffizientenmatrix die Anzahl der Lösungen für das Gleichungssystem
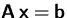 .
.
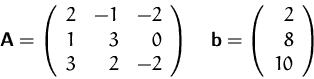
- (b)
- Lösen Sie das Gleichungssystem
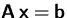 .
. - (c)
- Berechnen Sie die Determinante von
 .
. - (d)
- Ist
 invertierbar? Begründen Sie Ihre Antwort.
invertierbar? Begründen Sie Ihre Antwort.
(Lösung)
Bestimmen Sie die Bereiche in denen die Funktion
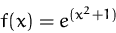
elastisch, 1-elastisch bzw. unelastisch ist.
(Lösung)
Bestimmen Sie die stationären Punkte für
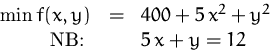
mit Hilfe der Lagrange-Multiplikatoren.
(Lösung)
Lösen Sie die Optimierungsaufgabe
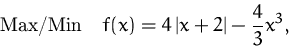
wobei 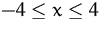 .
.(Lösung)
Lösen Sie die Differentialgleichung
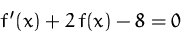
mit der Anfangsbedingung 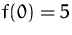 .
.(Lösung)
- (a)
- Bestimmen Sie die stationären Punkte der Funktion:
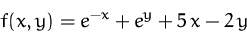
- (b)
- Stellen Sie mit Hilfe der Hessematrix fest, ob es sich bei den
stationären Punkten um lokale Minima, lokale Maxima oder
Sattelpunkte handelt.
(Lösung)
- (a)
- Lösen Sie graphisch das folgende lineare Optimierungsproblem:
![\begin{displaymath}
\begin{array}
{rr}
\min/\max & 4\,x_1 + 2\,x_2\\ [1ex]
\mb...
...eq 6 \\ & x_1 + x_2 \leq 8 \\ & x_1, x_2 \geq 0
\end{array} \end{displaymath}](img11.gif)
- (b)
- Wie ändert sich die Lösung durch das Hinzufügen der weiteren
Nebenbedingung:
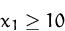
(Lösung)
Berechnen Sie 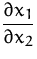 der
impliziten Funktion:
der
impliziten Funktion:
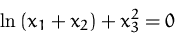
(Lösung)
- (a)
- Berechnen Sie die Determinante der Matrix:
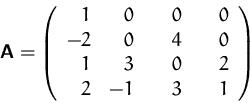
- (b)
- Berechnen Sie unter zu Hilfenahme der Determinante von
 die
Determinaten der folgenden zwei Matrizen.
die
Determinaten der folgenden zwei Matrizen.
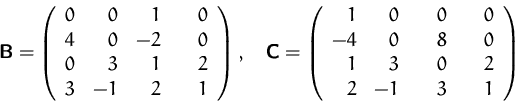
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
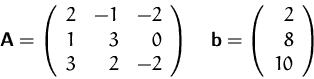
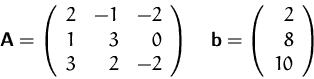
![]()
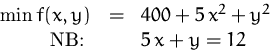
![]()
![]()
![]()
![\begin{displaymath}
\begin{array}
{rr}
\min/\max & 4\,x_1 + 2\,x_2\\ [1ex]
\mb...
...eq 6 \\ & x_1 + x_2 \leq 8 \\ & x_1, x_2 \geq 0
\end{array} \end{displaymath}](img11.gif)
![]()
![]()
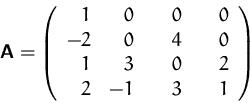
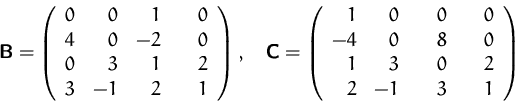
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)