

previous: 29. September 1997
next: 22. April 1997
- (a)
- Berechnen sie
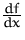 für
für
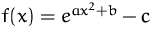 .
. - (b)
- Berechnen sie
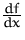 für
für
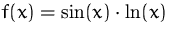 .
. - (c)
- Berechnen Sie
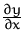 der impliziten Funktion
der impliziten Funktion
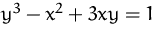 .
.
(Lösung)
Sei
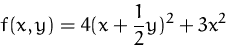
- (a)
- Berechnen Sie alle stationären Punkte von
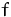 .
. - (b)
- Bestimmen Sie mit Hilfe der Hessematrix, ob es sich dabei um lokale
Minima, Maxima oder Sattelpunkte handelt.
- (c)
- Bestimmen Sie die Krümmung von
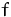 .
.
(Lösung)
Lösen sie die folgende Optimierungsaufgabe. (Gesucht sind alle
globalen Extrema.)
Min/Max
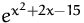
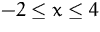
(Lösung)
- (a)
- Bestimmen Sie die Inverse der Matrix
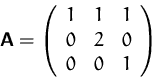
- (b)
- Überprüfen Sie das Ergebnis durch die Multiplikation
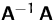 .
.
(Lösung)
Sei
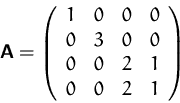
- (a)
- Berechnen Sie
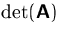 .
. - (b)
- Ist
 invertierbar?
invertierbar?
- (c)
- Ist
 singulär oder regulär?
singulär oder regulär?
- (d)
- Hat
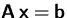 für
für
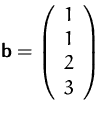 eine eindeutig bestimmte Lösung?
eine eindeutig bestimmte Lösung?
(Lösung)
Bestimmen Sie 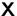 aus der Matrixgleichung
aus der Matrixgleichung
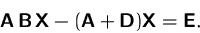
Gehen Sie davon aus, daß  ,
, 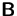 ,
, 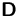 und
und 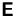 quadratische Matrizen gleicher Größe sind.
quadratische Matrizen gleicher Größe sind.
(Lösung)
Gegeben ist folgendes lineares Optimierungssystem
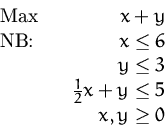
Lösen Sie das Optimierungsproblem graphisch.
(Lösung)
Bringen Sie das lineare Optimierungsproblem
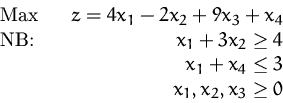
auf Standardform.
Hinweis: Die Lösung des Optimierungsproblems mit dem
Simplexalgorithmus ist nicht Teil der Aufgabenstellung.
(Lösung)
Ein Unternehmen erzeugt zwei Produkte 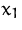 ,
, 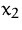 und verkauft diese zu
einem Preis
und verkauft diese zu
einem Preis 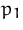 bzw.
bzw. 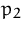 . Von Produkt
. Von Produkt 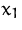 werden
werden 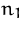 , von
Produkt
, von
Produkt 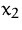
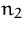 Stück verkauft.
Bei der Produktion fallen Produktionskosten
Stück verkauft.
Bei der Produktion fallen Produktionskosten 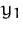 bzw.
bzw. 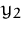 (pro Stück) an. Stellen Sie den Gewinn
(pro Stück) an. Stellen Sie den Gewinn 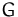 des Unternehmens
als mathematische Funktion der oben angeführten Größen dar.
des Unternehmens
als mathematische Funktion der oben angeführten Größen dar.
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
![]()
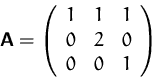
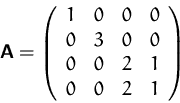
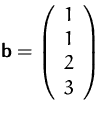 eine eindeutig bestimmte Lösung?
eine eindeutig bestimmte Lösung?
![]()
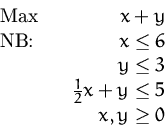
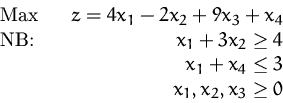
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)