

previous: 5. Oktober 1995
next: 2. Mai 1995
Suchen Sie das globale Maximum und Minimum der Funktion
(Lösung)
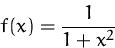
- (a)
- Bestimmen Sie die Elastizität von
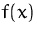 .
. - (b)
- Wo ist
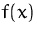 elastisch, unelastisch bzw. 1-elastisch?
elastisch, unelastisch bzw. 1-elastisch?
(Lösung)
- (a)
- Berechnen Sie die Determinate von
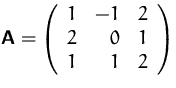
- (b)
- Ist das Gleichungssystem
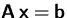 für
für
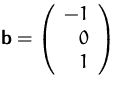 eindeutig lösbar?
eindeutig lösbar?
- (c)
- Berechnen Sie (mit Hilfe des Ergebnisses von (a)) die Determinante von
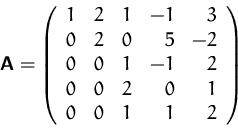
- (d)
- Sind die Spaltenvektoren der in (a) angegeben Matrix linear
unabhängig?
(Lösung)
Suchen Sie alle stationären Punkte der Funktion
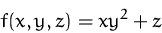
unter der Nebenbedingung
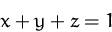
mittels Lagrangemultiplikatoren.
(Lösung)
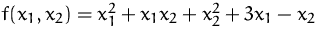
- (a)
- Bestimmen Sie alle stationären Punkte.
- (b)
- Stellen Sie mit Hilfe der Hessematrix fest, ob es sich bei den stationären
Punkten um Maxima, Minima oder Sattelpunkte handelt.
- (c)
- Können Sie Aussagen (mit Begründung!) über ein globales Minimum bzw.
Maximum machen?
(Lösung)
- (a)
-
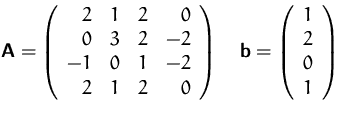
Bestimmen Sie die Lösung(en) des Gleichungssystems 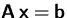 .
.
- (b)
- Berechnen Sie den Rang von
 .
.
(Lösung)
- (a)
- Invertieren Sie die Matrix
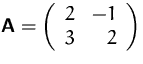
- (b)
- Überprüfen Sie, ob Sie
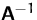 richtig berechnet haben.
richtig berechnet haben.
(Lösung)
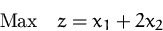
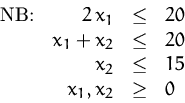
- (a)
- Lösen Sie das lineare Optimierungsproblem mit dem
Simplexalgorithmus.
- (b)
- Lösen Sie das Problem graphisch. Bezeichnen Sie die Eckpunkte,
die den mit dem Simplexalgorithmus erstellten Tableaus
entsprechen. (
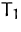 für das Starttableau,
für das Starttableau, 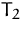 für das nächste
Tableau u.s.w.)
für das nächste
Tableau u.s.w.)
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
![]()
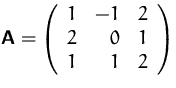
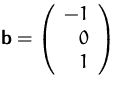 eindeutig lösbar?
eindeutig lösbar?
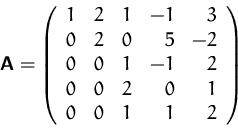
![]()
![]()
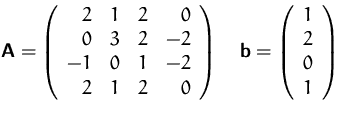
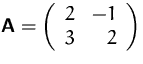
![]()
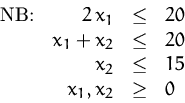
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)