

previous: 14. November 1995
next: 28. Juni 1995
- (a)
- Bestimmen Sie die Lösung(en) des Gleichungssystems
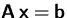 .
.
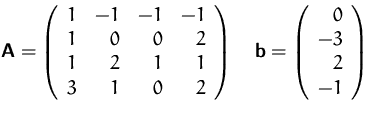
- (b)
- Welchen Rang hat die Matrix
 ?
?
(Lösung)
Suchen Sie alle stationären Punkte der Funktion
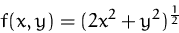
unter der Nebenbedingung
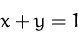
mittels Lagrange-Multiplikatoren.
(Lösung)
- (a)
- Bestimmen Sie die Determinante von
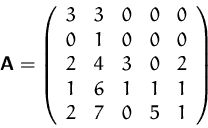
- (b)
- Bestimmen Sie die Determinante von
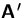 .
.
(Lösung)
Gegeben ist die Funktion
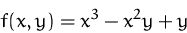
- (a)
- Bestimmen Sie alle stationären Punkte.
- (b)
- Stellen Sie mit Hilfe der Hesse-Matrix fest, ob es sich bei den
stationären Punkten um Maxima, Minima oder Sattelpunkte handelt.
(Lösung)
- (a)
- Berechnen Sie die Inverse
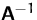 von
von
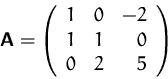
- (b)
- Überprüfen Sie, ob Sie
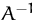 richtig berechnet haben.
richtig berechnet haben.
(Lösung)
Gegeben ist die Funktion

Bestimmen Sie den Definitionsbereich von 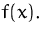
Skizzieren Sie die Funktion und bestimmen Sie anhand der Zeichnung und anderen Überlegungen, ob
die Funktion überall stetig und differenzierbar ist. Wenn nicht, geben Sie die Stellen an, an
denen die Funktion nicht stetig und/oder differenzierbar ist.
(Lösung)
Berechnen Sie 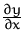 der impliziten Funktion
der impliziten Funktion
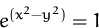
(Lösung)
Eine Firma will Inserate schalten, und hat dabei zwei Zeitschriften 1
und 2 zur Auswahl.
Ein solches Inserat wird in Zeitschrift 1 von 100 Personen, in
Zeitschrift 2 von 200 Personen gelesen. Die Firma will, daß ihre Inserate
möglichst oft gelesen werden, das heißt also, sie will die Anzahl
der Leser der Inserate maximieren.
Dabei gelten aber folgende Beschränkungen:
- (1)
- Die Firma kann insgesamt nur 20 Inserate schalten.
- (2)
- Die Firma hat ein Budget von 30 000 ATS. Ein Inserat
in Zeitschrift 1 kostet 1000 ATS, in Zeitung 2 dagegen
3000 ATS.
- (3)
- Die Firma muß in Zeitung 1 mindestens 2 Inserate schalten (weil der
Redakteur ein Freund vom Besitzer ist).
- (a)
- Schreiben Sie das Problem als lineares Optimierungsproblem an
und lösen Sie es graphisch.
- (b)
- Lösen Sie das Problem mit Hilfe des
Simplexalgorithmus. (Streichen Sie dabei die Nebenbedinung (3).)
(Lösung)
Bestimmen Sie die Elastizität der Funktion.
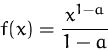
- (a)
- Berechnen Sie die Elastizität der Funktion.
- (b)
- Bestimmen Sie die Bereiche, in denen die Funktion elastisch bzw. unelastisch ist.
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
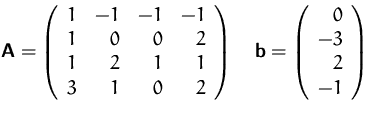
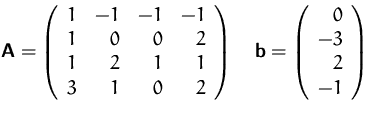
![]()
![]()
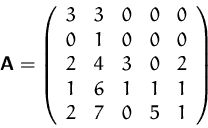
![]()
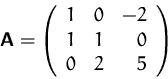

![]()
![]()
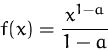
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)