

previous: 28. Juni 1995
next: Lösung zu Aufgabe 1
- (a)
- Invertieren Sie die Matrix
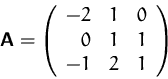
- (b)
- Überprüfen Sie, ob Sie die Matrix
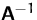 richtig berechnet haben?
richtig berechnet haben?
- (c)
- Welchen Rang hat
 ?
?
(Lösung)
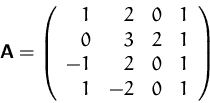
- (a)
- Berechnen Sie die Determinante von
 .
. - (b)
- Ist das Gleichungssystem
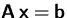 für
für
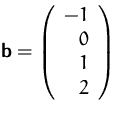 eindeutig
lösbar?
eindeutig
lösbar?
Verwenden Sie als Begründung das Resultat von (a).
(Lösung)
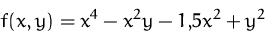
- (a)
- Berechnen Sie alle stationären Punkte von
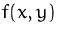 .
. - (b)
- Stellen Sie mit Hilfe der Hessematrix fest, ob es sich um
lokale Minima, Maxima oder Sattelpunkte handelt.
(Lösung)
Bestimmen Sie die Lösung(en) des Gleichungssystems:
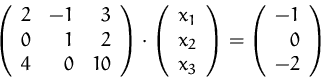
(Lösung)
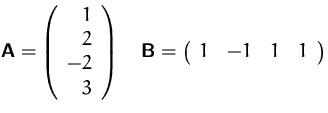
- (a)
- Berechnen Sie (wenn möglich) die Matrix
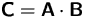
- (b)
- Wie groß ist der Rang von
 ?
?
(Lösung)
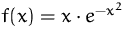
- (a)
- Bestimmen Sie die Elastizität von
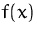 .
. - (b)
- Bestimmen Sie die Bereiche, in denen
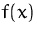 elastisch,
unelastisch oder 1-elastisch ist.
elastisch,
unelastisch oder 1-elastisch ist.
(Lösung)
Skizieren Sie 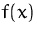 und stellen Sie mit Hilfe der Zeichnung (oder mit
anderen Überlegungen) fest, ob die Funktion überall stetig und überall
differenzierbar ist. Wenn nicht, geben Sie die Stellen an, an denen die
Funktion nicht stetig und/oder nicht differenzierbar ist.
und stellen Sie mit Hilfe der Zeichnung (oder mit
anderen Überlegungen) fest, ob die Funktion überall stetig und überall
differenzierbar ist. Wenn nicht, geben Sie die Stellen an, an denen die
Funktion nicht stetig und/oder nicht differenzierbar ist.
(Lösung)
Suchen Sie die stationären Punkte der Funktion
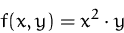
unter der Nebenbedingung
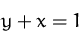
(Lösung)
Bestimmen Sie Minimum und Maximum des linearen Optimierungsproblems mit
der graphischen Methode.
Min/Max 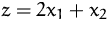
NB: 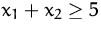
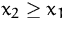
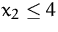
(Lösung)
Eine Firma produziert 2 Produkte 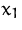 und
und 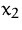 .
.
Eine Tonne von Produkt 1 hat einen Preis von 1000, eine Tonne von Produkt 2
hat einen Preis von
1500 Geldeinheiten.
Maschine A ist 8 Stunden in Betrieb und wird für eine Tonne von Produkt
1 und eine Tonne von Produkt 2 jeweils eine Stunde benötigt.
Maschine B ist täglich 10 Stunden in Betrieb und wird für 1 Tonne von
Produkt 1 eine Stunde, für 1 Tonne von Produkt 2 eineinhalb Stunden
benötigt.
Eine strategische Enscheidung der Firmenleitung besagt, daß von Produkt 2
höchstens gleich viel wie von Produkt 1 produziert werden darf.
Formulieren Sie das lineare Optimierungsproblem, mit dem der Umsatz
maximiert werden kann.
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
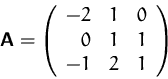
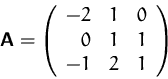
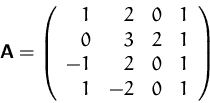
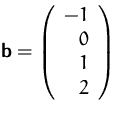 eindeutig
lösbar?
eindeutig
lösbar?
![]()
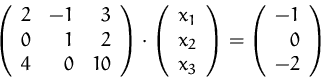
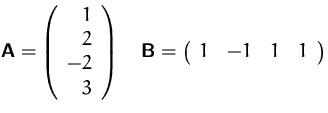
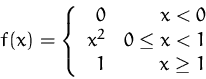
![]()
![]()
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)