

previous: 26. Juni 1996
next: 25. Jänner 1996
Gegeben ist die Matrixgleichung
- (a)
- Geben Sie an, welche Beschränkungen es für die Zeilenzahl,
Spaltenzahl und Inventierbarkeit von
 ,
, 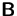 und
und 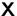 gibt, so daß
die Rechenoperationen in der Gleichung definiert sind und die
Gleichung nach
gibt, so daß
die Rechenoperationen in der Gleichung definiert sind und die
Gleichung nach 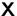 lösbar ist.
lösbar ist.
- (b)
- Lösen Sie die Gleichung nach
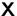 auf.
auf.
(Lösung)
Berechnen Sie mit dem Simplexalorithmus.
(Lösung)
Bestimmen Sie die stationären Punkte der Funktion
unter den Nebenbedingungen
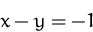
(Lösung)
Bestimmen Sie 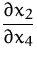 aus der impliziten Funktion:
aus der impliziten Funktion:
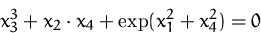
(Lösung)
Sei
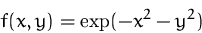
- (a)
- Berechnen Sie die stationären Punkte von
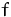 .
. - (b)
- Bestimmen Sie mit Hilfe der Hessematrix ob es sich dabei um
Maxima, Minima oder Sattelpunkte handelt.
- (c)
- Ist
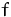 in
in 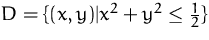
konvex, konkav oder keines von beiden? (Begründung)
- (d)
- Was können Sie über die globalen Extremwerte von
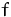 in
in  sagen?
sagen?
(Lösung)
Sei
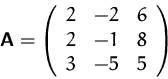
- (a)
- Berechnen Sie
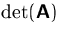 .
. - (b)
- Berechnen Sie den Rang von
 .
. - (c)
- Sind die Zeilenvektoren von
 linear unabhängig?
(Begründung)
linear unabhängig?
(Begründung)
- (d)
- Ist
 inventierbar? (Begründung)
inventierbar? (Begründung)
- (e)
- Lösen Sie das lineare Gleichungssystem
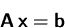
mit
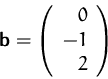
- (f)
- Berechnen Sie die inverse Matrix von
 .
.
(Lösung)
- (a)
- Berechnen Sie die Elastizität von
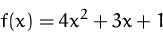
- (b)
- In welchen Punkten ist
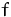 1-elastisch.
1-elastisch.
- (c)
- In welchem Bereich ist
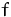 elastisch.
elastisch.
(Lösung)
- (a)
- Berechnen Sie das Differential der Funktion
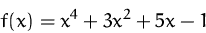
an der Stelle 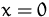 .
. - (b)
- Berechnen Sie mit Hilfe des Differentials and der Stelle
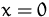 ein
Näherungswert für den Funktionswert von
ein
Näherungswert für den Funktionswert von 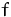 in den Punkten
0,1 und 0,2.
in den Punkten
0,1 und 0,2.
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
![]()
![]()
![]()
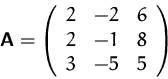
![]()
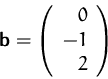
![]()
![]()
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)